IX. Exercices▲
Les exercices sont de difficulté variable, de ★ (simple) à ★★★ (complexe).
IX-A. Introduction▲
IX-A-1. Intégration : méthode des rectangles ★▲
La méthode des rectangles permet d'approximer numériquement l'intégrale d'une fonction f :
kitxmlcodelatexdvp\int_a^b f(x)\,\mathrm{d}x \approx h \sum_{i=0}^{n-1} f(x_{i}) \quad\text{avec}\quad h = (b-a)/n \quad\text{et}\quad x_i = a + (i+1/2)h.finkitxmlcodelatexdvpOn définit la fonction sq renvoyant le carré d'un nombre par (cf. FonctionsFonctions) :
def sq(x) :
return x*xÉcrire un programme calculant l'intégrale de cette fonction entre a=0 et b=1, en utilisant une subdivision en n=100 pas dans un premier temps. Quelle est la précision de la méthode, et comment dépend-elle du nombre de pas ?
IX-A-2. Fizz Buzz ★▲
Écrire un programme jouant au Fizz Buzz jusqu'à 99 :
1 2 Fizz! 4 Buzz! Fizz! 7 8 Fizz! Buzz! 11 Fizz! 13 14 Fizz Buzz! 16...IX-A-3. PGCD : algorithme d'Euclide ★★▲
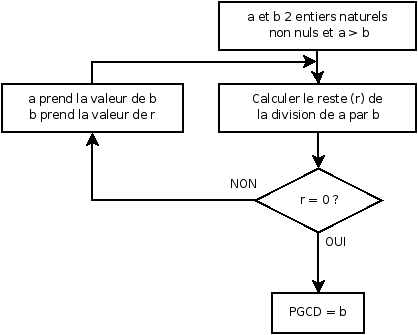
Écrire un programme calculant le PGCDPlus Grand Commun Dénominateur de deux nombres (p.ex. 306 et 756) par l'algorithme d'Euclide.
IX-A-4. Tables de multiplication ★▲
Écrire un programme affichant les tables de multiplication :
2.
3.
4.
1 x 1 = 1
1 x 2 = 2
...
9 x 9 = 81
IX-B. Manipulation de listes▲
IX-B-1. Crible d'Ératosthène ★▲
Implémenter le crible d'Ératosthène pour afficher les nombres premiers compris entre 1 et un entier fixe, p.ex. :
Liste des entiers premiers <= 41
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41]IX-B-2. Carré magique ★★▲
Un carré magique d'ordre n est un tableau carré n × n dans lequel on écrit une et une seule fois les nombres entiers de 1 à n², de sorte que la somme des n nombres de chaque ligne, colonne ou diagonale principale soit constante. P.ex. le carré magique d'ordre 5, où toutes les sommes sont égales à 65 :
|
11 |
18 |
25 |
2 |
9 |
|
10 |
12 |
19 |
21 |
3 |
|
4 |
6 |
13 |
20 |
22 |
|
23 |
5 |
7 |
14 |
16 |
|
17 |
24 |
1 |
8 |
15 |
Pour les carrés magiques d'ordre impair, on dispose de l'algorithme suivant - (i,j) désignant la case de la ligne i, colonne j du carré ; on se place en outre dans une indexation « naturelle » commençant à 1 :
- La case (n,(n+1)/2) contient 1 ;
- Si la case (i,j) contient la valeur k, alors on place la valeur k+1 dans la case (i+1,j+1) si cette case est vide, ou dans la case (i-1,j) sinon. On respecte la règle selon laquelle un indice supérieur à n est ramené à 1.
Programmer cet algorithme pour pouvoir construire un carré magique d'ordre impair quelconque.
IX-C. Programmation▲
IX-C-1. Suite de Syracuse (fonction) ★▲
Écrire une fonction suite_syracuse(n) retournant la (partie non triviale de la) suite de Syracuse pour un entier n. Écrire une fonction temps_syracuse(n, altitude=False) retournant le temps de vol (éventuellement en altitude) correspondant à l'entier n. Tester ces fonctions sur n=15 :
2.
3.
4.
5.
6.
>>> suite_syracuse(15)
[15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
>>> temps_syracuse(15)
17
>>> temps_syracuse(15, altitude=True)
10
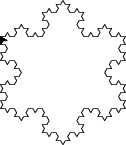
IX-C-2. Flocon de Koch (programmation récursive) ★★★▲
En utilisant les commandes left, right et forward de la bibliothèque graphique standard turtle dans une fonction récursive, générer à l'écran un flocon de Koch d'ordre arbitraire.
IX-C-3. Jeu du plus ou moins (exceptions) ★▲
Écrire un jeu de « plus ou moins »:
2.
3.
4.
5.
Vous devez deviner un nombre entre 1 et 100.
Votre proposition: 27
C'est plus.
[...]
Vous avez trouvé en 6 coups !
La solution sera générée aléatoirement par la fonction random.randint(). Le programme devra être robuste aux entrées invalides (« toto », 120, etc.), et aux lâches abandons par interruption (KeyboardInterrupt).
IX-C-4. Animaux (POO/TDD) ★▲
Téléchargez animaux.py et complétez les classes Animal et Chien pour qu'elles passent avec succès tous les tests (voir Développement piloté par les testsDéveloppement piloté par les tests). On appellera les tests via la ligne de commande :
py.test animaux.pyIX-C-5. Jeu de la vie (POO) ★★▲
On se propose de programmer l'automate cellulaire le plus célèbre, le Jeu de la vie.
Pour cela, vous créerez une classe Life qui contiendra la grille du jeu ainsi que les méthodes qui permettront son évolution. Vous initialiserez la grille aléatoirement à l'aide de la fonction random.choice(), et vous afficherez l'évolution de l'automate dans la sortie standard du terminal, p.ex. :
2.
3.
4.
5.
6.
7.
8.
9.
...#..#.....##.......
.....###.............
#........#...........
.....#...#...........
................##...
.....#.#......##..#..
..............##.##..
..............##.##..
................#....
Pour que l'affichage soit agréable à l'œil, vous marquerez des pauses entre l'affichage de chaque itération grâce à la fonction time.sleep().
IX-D. Manipulation de tableaux (arrays)▲
IX-D-1. Inversion de matrice ★▲
Créer un tableau carré réel rr\mathsf{r} aléatoire (numpy.random.randn()), calculer la matrice hermitienne kitxmlcodeinlinelatexdvp\mathsf{m} = \mathsf{r} \cdot \mathsf{r}^Tfinkitxmlcodeinlinelatexdvp (numpy.dot()), l'inverser (numpy.linalg.inv()), et vérifier que kitxmlcodeinlinelatexdvp\mathsf{m} \cdot \mathsf{m}^{-1} = \mathsf{m}^{-1} \cdot \mathsf{m} = \mathsf{1}finkitxmlcodeinlinelatexdvp (numpy.eye()) à la précision numérique près (numpy.allclose()).
IX-D-2. Median Absolute Deviation ★▲
En statistique, le Median Absolute Deviation (MAD) est un estimateur robuste de la dispersion d'un échantillon 1D : MAD = median(| x - median(x) |).
À l'aide des fonctions numpy.median() et numpy.abs(), écrire une fonction mad(x, axis=None) calculant le MAD d'un tableau, éventuellement le long d'un ou plusieurs de ses axes.
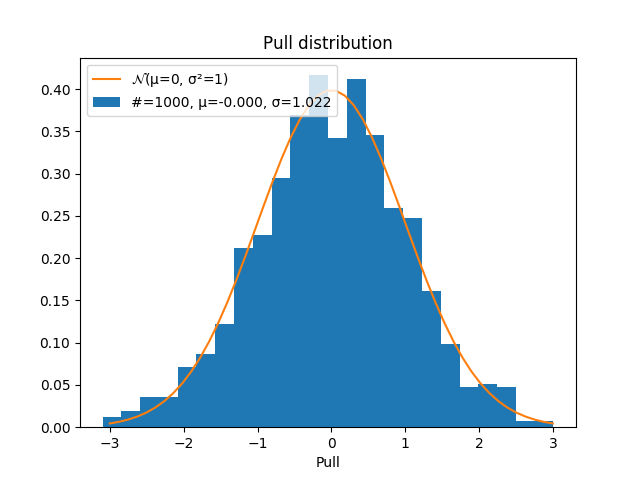
IX-D-3. Distribution du pull ★★★▲
Le pull est une quantité statistique permettant d'évaluer la conformité des erreurs par rapport à une distribution de valeurs (typiquement les résidus d'un ajustement). Pour un échantillon kitxmlcodeinlinelatexdvp\mathbf{x} = [x_i]finkitxmlcodeinlinelatexdvp et les erreurs associées kitxmlcodeinlinelatexdvp\mathrm{d}\mathbf{x} = [\sigma_i]finkitxmlcodeinlinelatexdvp, le pull est défini par :
- moyenne optimale (pondérée par la variance) : kitxmlcodeinlinelatexdvpE = (\sum_{i} x_i/\sigma_i^2)/(\sum_i 1/\sigma_i^2)finkitxmlcodeinlinelatexdvp ;
- erreur sur la moyenne pondérée : kitxmlcodeinlinelatexdvp\sigma_E^2 = 1/\sum(1/\sigma_i^2)finkitxmlcodeinlinelatexdvp ;
- définition du pull : kitxmlcodeinlinelatexdvp\sigma_E^2 = 1/\sum(1/\sigma_i^2)finkitxmlcodeinlinelatexdvp, où kitxmlcodeinlinelatexdvpE_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\sigma_{E_i}finkitxmlcodeinlinelatexdvp sont calculées sans le point i.
Si les erreurs kitxmlcodeinlinelatexdvp\sigma_ifinkitxmlcodeinlinelatexdvp sont correctes, la distribution du pull est centrée sur 0 avec une déviation standard de 1.
Écrire une fonction pull(x, dx) calculant le pull de tableaux 1D.
IX-E. Méthodes numériques▲
IX-E-1. Quadrature et zéro d'une fonction ★▲
À l'aide des algorithmes disponibles dans scipy :
- calculer numériquement l'intégrale kitxmlcodeinlinelatexdvp\int_0^\infty \frac{x^3}{e^x-1}\mathrm{d}x = \pi^4/15finkitxmlcodeinlinelatexdvp ;
- résoudre numériquement l'équation kitxmlcodeinlinelatexdvpx\,e^x = 5(e^x - 1)finkitxmlcodeinlinelatexdvp.
IX-E-2. Schéma de Romberg ★★▲
Écrire une fonction integ_romberg(f, a, b, epsilon=1e-6) permettant de calculer l'intégrale numérique de la fonction f entre les bornes a et b avec une précision epsilon selon la méthode de Romberg.
Tester sur des solutions analytiques et en comparant à scipy.integrate.romberg().
IX-E-3. Méthode de Runge-Kutta ★★▲
Développer un algorithme permettant d'intégrer numériquement une équation différentielle du 1er ordre en utilisant la méthode de Runge-Kutta d'ordre quatre.
Tester sur des solutions analytiques et en comparant à scipy.integrate.odeint().
IX-F. Visualisation (matplotlib)▲
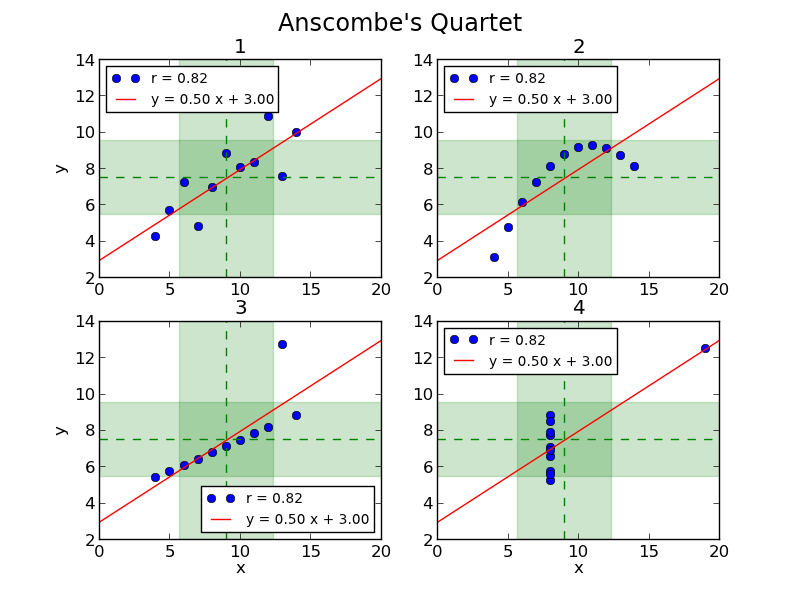
IX-F-1. Quartet d'Anscombe ★▲
Après chargement des données, calculer et afficher les propriétés statistiques des quatre jeux de données du Quartet d'Anscombe :
- moyenne et variance des x et des y (numpy.mean() et numpy.var()) ;
- corrélation entre les x et les y (scipy.stats.pearsonr()) ;
- équation de la droite de régression linéaire y = ax + b (scipy.stats.linregress())
|
I |
II |
III |
IV |
||||
|---|---|---|---|---|---|---|---|
|
x |
y |
x |
y |
x |
y |
x |
y |
|
10.0 |
8.04 |
10.0 |
9.14 |
10.0 |
7.46 |
8.0 |
6.58 |
|
8.0 |
6.95 |
8.0 |
8.14 |
8.0 |
6.77 |
8.0 |
5.76 |
|
13.0 |
7.58 |
13.0 |
8.74 |
13.0 |
12.74 |
8.0 |
7.71 |
|
9.0 |
8.81 |
9.0 |
8.77 |
9.0 |
7.11 |
8.0 |
8.84 |
|
11.0 |
8.33 |
11.0 |
9.26 |
11.0 |
7.81 |
8.0 |
8.47 |
|
14.0 |
9.96 |
14.0 |
8.10 |
14.0 |
8.84 |
8.0 |
7.04 |
|
6.0 |
7.24 |
6.0 |
6.13 |
6.0 |
6.08 |
8.0 |
5.25 |
|
4.0 |
4.26 |
4.0 |
3.10 |
4.0 |
5.39 |
19.0 |
12.50 |
|
12.0 |
10.84 |
12.0 |
9.13 |
12.0 |
8.15 |
8.0 |
5.56 |
|
7.0 |
4.82 |
7.0 |
7.26 |
7.0 |
6.42 |
8.0 |
7.91 |
|
5.0 |
5.68 |
5.0 |
4.74 |
5.0 |
5.73 |
8.0 |
6.89 |
Pour chacun des jeux de données, tracer y en fonction de x, ainsi que la droite de régression linéaire.
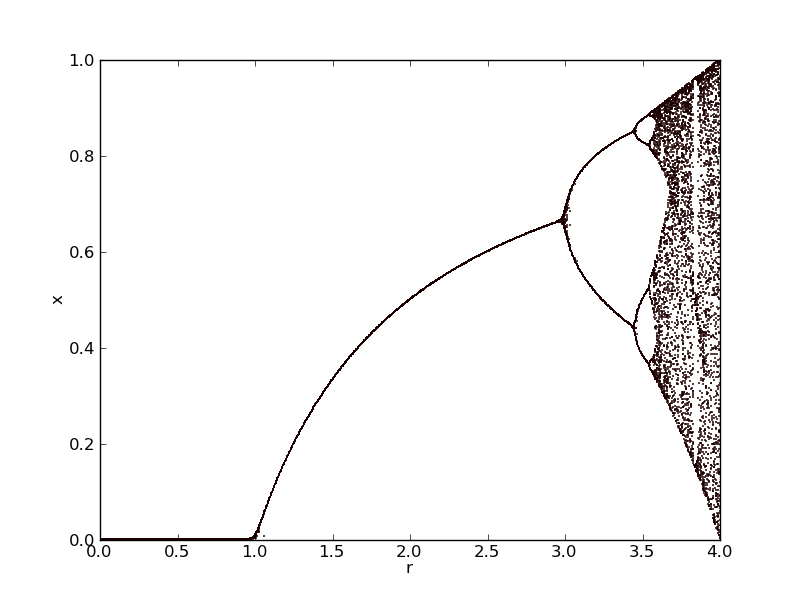
IX-F-2. Diagramme de bifurcation : la suite logistique ★★▲
Écrivez une fonction qui calcule la valeur d'équilibre de la suite logistique pour un kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp (nécessairement compris entre 0 et 1) et un paramètre kitxmlcodeinlinelatexdvprfinkitxmlcodeinlinelatexdvp (parfois noté kitxmlcodeinlinelatexdvp\mufinkitxmlcodeinlinelatexdvp) donné.
Générez l'ensemble de ces points d'équilibre pour des valeurs de kitxmlcodeinlinelatexdvprfinkitxmlcodeinlinelatexdvp comprises entre 0 et 4 :
N.B. Vous utiliserez la bibliothèque MatplotlibMatplotlib pour tracer vos résultats.
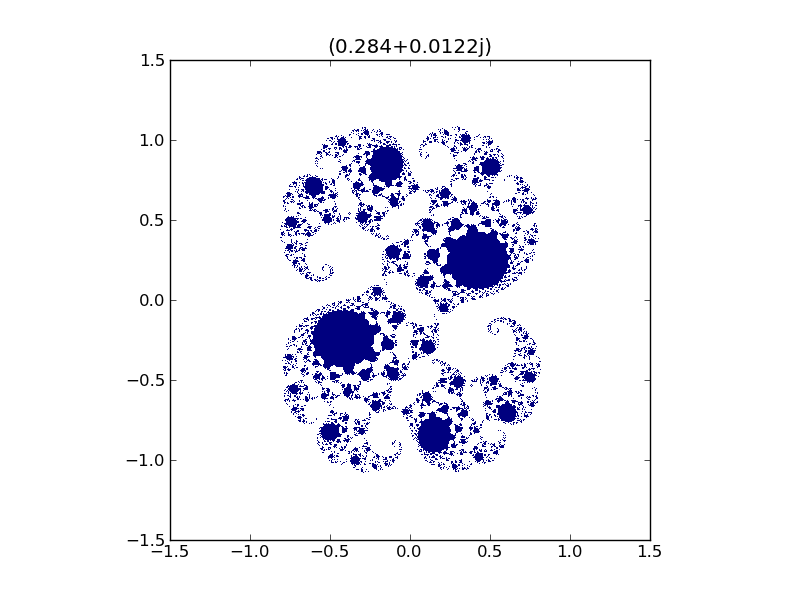
IX-F-3. Ensemble de Julia ★★▲
Représentez l'ensemble de Julia pour la constante complexe kitxmlcodeinlinelatexdvpc = 0.284 + 0.0122jfinkitxmlcodeinlinelatexdvp :
On utilisera la fonction numpy.meshgrid() pour construire le plan complexe, et l'on affichera le résultat grâce à la fonction matplotlib.pyplot.imshow().
Voir également : Superposition d'ensembles de Julia
IX-G. Mise en œuvre de l'ensemble des connaissances acquises▲
IX-G-1. Équation différentielle ★▲
À l'aide de la fonction scipy.integrate.odeint(), intégrer les équations du mouvement d'un boulet de canon soumis à des forces de frottement « turbulentes » (en kitxmlcodeinlinelatexdvpv^2finkitxmlcodeinlinelatexdvp) :
kitxmlcodelatexdvp\ddot{\mathbf{r}} = \mathbf{g} - \frac{\alpha}{m}v\times\mathbf{v}.finkitxmlcodelatexdvpUtiliser les valeurs numériques pour un boulet de canon de 36 livres :
2.
3.
4.
5.
6.
7.
8.
9.
g = 9.81 # Pesanteur [m/s2]
cx = 0.45 # Coefficient de frottement d'une sphère
rhoAir = 1.2 # Masse volumique de l'air [kg/m3]
rad = 0.1748/2 # Rayon du boulet [m]
rho = 6.23e3 # Masse volumique du boulet [kg/m3]
mass = 4./3.*N.pi*rad**3 * rho # Masse du boulet [kg]
alpha = 0.5*cx*rhoAir*N.pi*rad**2 / mass # Coeff. de frottement / masse
v0 = 450. # Vitesse initiale [m/s]
alt = 45. # Inclinaison du canon [deg]
IX-H. Exercices en vrac▲
X. Solutions aux exercices▲
X-A. Méthode des rectangles▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2014-09-17 19:30:18 ycopin>
# Division réelle de type Python 3 - ligne admise
from __future__ import division
"""
Définition de la fonction carré et calcul de son intégrale entre 0
et 1 dans le main par la méthode des rectangles (subdivision en 100
pas)
"""
__author__ = "Adrien Licari <adrien.licari@ens-lyon.fr>"
# Définition de la fonction sq, admise au stade du TD 1
def sq(x):
return x * x
# Début du programme principal (main)
# On définit les bornes d'intégration a et b, le nombre de pas n
a = 0
b = 1
n = 100
# Largeur des rectangles dx
h = (b - a) / n # Division réelle!
integ = 0 # Cette variable accumulera les aires des rectangles
# On sait déjà que l'on va calculer n aires de rectangles, donc une
# boucle for est appropriée
for i in range(n): # Boucle de 0 à n-1
x = a + (i + 0.5) * h # Abscisse du rectangle
integ += sq(x) * h # On ajoute au total l'aire du rectangle
print "Intégrale de x**2 entre a =", a, "et b =", b, "avec n =", n
# On affiche le résultat numérique
print "Résultat numérique: ", integ
theorie = (b ** 3 - a ** 3) / 3 # Résultat analytique
# On affiche le résultat analytique
print "Résultat analytique:", theorie
print "Erreur relative:", (integ / theorie - 1) # On affiche l'erreur
$ python integ.py
Intégrale de x**2 entre a = 0 et b = 1 avec n = 100
Résultat numérique: 0.333325
Résultat analytique: 0.333333333333
Erreur relative: -2.49999999998e-05Source : integ.py
X-B. Fizz Buzz▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2017-05-28 21:42 ycopin@lyonovae03.in2p3.fr>
"""
Jeu du Fizz Buzz
"""
__author__ = "Yannick Copin <y.copin@ipnl.in2p3.fr>"
for i in range(1, 100): # Entiers de 1 à 99
if ((i % 3) == 0) and ((i % 5) == 0): # Multiple de 3 et 5
print 'Fizz Buzz!', # Affichage sans retour à la ligne
elif ((i % 3) == 0): # Multiple de 3 uniquement
print 'Fizz!',
elif ((i % 5) == 0): # Multiple de 5 uniquement
print 'Buzz!',
else:
print i,
$ python fizz.py
1 2 Fizz! 4 Buzz! Fizz! 7 8 Fizz! Buzz! 11 Fizz! 13 14 Fizz Buzz! 16...Source : fizz.py
X-C. Algorithme d'Euclide▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2014-09-17 18:25:00 ycopin>
"""
Calcul du PGCD de deux entiers
"""
__author__ = "Adrien Licari <adrien.licari@ens-lyon.fr>"
# Entiers dont on calcule le PGCD
a = 306
b = 756
# Test usuels : les nombres sont bien positifs et a > b
assert a > 0
assert b > 0
if (a < b):
a, b = b, a # Interversion
a0, b0 = a, b # On garde une copie des valeurs originales
# On boucle jusqu'à ce que le reste soit nul, d'où la boucle while. Il
# faut être sûr que l'algorithme converge dans tous les cas !
while (b != 0):
# On remplace a par b et b par le reste de la division euclidienne
# de a par b
a, b = b, a % b
print 'Le PGCD de', a0, 'et', b0, 'vaut', a # On affiche le résultat
# Vérifications
print a0 // a, 'x', a, '=', (a0 // a * a) # a//b: division euclidienne
print b0 // a, 'x', a, '=', (b0 // a * a)
$ python pgcd.py
Le PGCD de 756 et 306 vaut 18
42 x 18 = 756
17 x 18 = 306Source : pgcd.py
X-D. Crible d'Ératosthène▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Crible d'Ératosthène.
Source: http://fr.wikibooks.org/wiki/Exemples_de_scripts_Python#Implémentation_du_crible_d'Ératosthène
"""
__author__ = "Yannick Copin <y.copin@ipnl.in2p3.fr>"
# start-sys
# Gestion simplifiée d'un argument entier sur la ligne de commande
import sys
if sys.argv[1:]: # Présence d'au moins un argument sur la ligne de commande
try:
n = int(sys.argv[1]) # Essayer de lire le 1er argument comme un entier
except ValueError:
raise ValueError("L'argument '{}' n'est pas un entier"
.format(sys.argv[1]))
else: # Pas d'argument sur la ligne de commande
n = 101 # Valeur par défaut
# end-sys
# Liste des entiers *potentiellement* premiers. Les nb non premiers
# seront étiquetés par 0 au fur et à mesure.
l = range(n + 1) # <0,...,n>, 0 n'est pas premier
l[1] = 0 # 1 n'est pas premier
i = 2 # Entier à tester
while i ** 2 <= n: # Inutile de tester jusqu'à n
if l[i] != 0: # Si i n'est pas étiqueté (=0)...
# ...étiqueter tous les multiples de i
l[2 * i::i] = [0] * len(l[2 * i::i])
i += 1 # Passer à l'entier à tester suivant
# Afficher la liste des entiers premiers (c-à-d non étiquetés)
print "Liste des entiers premiers <= {} :".format(n)
print [i for i in l if i != 0]
$ python crible.py
Liste des entiers premiers <= 101
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101]Source : crible.py
X-E. Carré magique▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2017-07-13 14:29 ycopin@lyonovae03.in2p3.fr>
"""
Création et affichage d'un carré magique d'ordre impair.
"""
__author__ = "Yannick Copin <y.copin@ipnl.in2p3.fr>"
n = 5 # Ordre du carré magique
# On vérifie que l'ordre est bien impair
assert n % 2 == 1, "L'ordre {} n'est pas impair".format(n)
# Le carré sera stocké dans une liste de n listes de n entiers
# Initialisation du carré: liste de n listes de n zéros.
array = [[0 for j in range(n)] for i in range(n)]
# Initialisation de l'algorithme
i, j = n, (n + 1) / 2 # Indices de l'algo (1-indexation)
array[i - 1][j - 1] = 1 # Attention: python utilise une 0-indexation
# Boucle sur valeurs restant à inclure dans le carré (de 2 à n**2)
for k in range(2, n**2 + 1):
# Test de la case i+1, j+1 (modulo n)
i2 = (i + 1) % n
j2 = (j + 1) % n
if array[i2 - 1][j2 - 1] == 0: # La case est vide: l'utiliser
i, j = i2, j2
# La case est déjà remplie : utiliser la case i-1, j
else:
i = (i - 1) % n
array[i - 1][j - 1] = k # Remplissage de la case
# Affichage, avec vérification des sommes par ligne et par colonne
print "Carré magique d'ordre {}:".format(n)
for row in array:
print ' '.join('{:2d}'.format(k) for k in row), '=', sum(row)
print ' '.join('==' for k in row)
print ' '.join(str(sum(array[i][j] for i in range(n))) for j in range(n))
$ python carre.py
$ python carre.py
Carré magique d'ordre 5:
11 18 25 2 9 = 65
10 12 19 21 3 = 65
4 6 13 20 22 = 65
23 5 7 14 16 = 65
17 24 1 8 15 = 65
== == == == ==
65 65 65 65 65Source : carre.py
X-F. Suite de Syracuse▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2014-09-24 17:31:53 ycopin>
__author__ = "Adrien Licari <adrien.licari@ens-lyon.fr>; Yannick Copin <y.copin@ipnl.in2p3.fr>"
def suite_syracuse(n):
"""
Retourne la suite de Syracuse pour l'entier n.
>>> suite_syracuse(15)
[15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
"""
seq = [n] # La suite de Syracuse sera complétée...
while (seq[-1] != 1): # ...jusqu'à tomber sur 1
if seq[-1] % 2 == 0: # u_n est pair
seq.append(seq[-1] // 2) # Division euclidienne par 2
else: # u_n est impair
seq.append(seq[-1] * 3 + 1)
return seq
def temps_syracuse(n, altitude=False):
"""
Calcule le temps de vol (éventuellement en altitude) de la suite
de Syracuse pour l'entier n.
>>> temps_syracuse(15)
17
>>> temps_syracuse(15, altitude=True)
10
"""
seq = suite_syracuse(n)
if not altitude: # Temps de vol total
return len(seq) - 1
else: # Temps de vol en altitude
# Construction de la séquence en altitude
alt = []
for i in seq:
if i >= n:
alt.append(i)
else:
break
return len(alt) - 1
if __name__ == '__main__':
n = 15
print "Suite de Syracuse pour n =", n
print suite_syracuse(n)
print "Temps de vol total: ", temps_syracuse(n)
print "Temps de vol en altitude:", temps_syracuse(n, altitude=True)
Suite de Syracuse pour n = 15
[15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
Temps de vol total: 17
Temps de vol en altitude: 10Source : syracuse.py
X-G. Flocon de Koch▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from __future__ import division # Pas de division euclidienne par défaut
"""
Tracé (via 'turtle') d'un flocon de Koch d'ordre arbitraire.
Dans le même genre:
- courbe de Peano (http://fr.wikipedia.org/wiki/Courbe_de_Peano)
- courbe de Hilbert (http://fr.wikipedia.org/wiki/Courbe_de_Hilbert)
- île de Gosper (http://fr.wikipedia.org/wiki/Île_de_Gosper)
Voir également:
- L-système: http://fr.wikipedia.org/wiki/L-système
- Autres exemples: http://natesoares.com/tutorials/python-fractals/
"""
__version__ = "Time-stamp: <2013-01-14 00:49 ycopin@lyopc469>"
__author__ = "Yannick Copin <y.copin@ipnl.in2p3.fr>"
import turtle as T
def koch(niveau=3, iter=0, taille=100, delta=0):
"""
Tracé du flocon de Koch de niveau 'niveau', de taille 'taille'
(px).
Cette fonction récursive permet d'initialiser le flocon (iter=0,
par défaut), de tracer les branches fractales (0<iter<=niveau) ou
bien juste de tracer un segment (iter>niveau).
"""
if iter == 0: # Dessine le triangle de niveau 0
T.title("Flocon de Koch - niveau {}".format(niveau))
koch(iter=1, niveau=niveau, taille=taille, delta=delta)
T.right(120)
koch(iter=1, niveau=niveau, taille=taille, delta=delta)
T.right(120)
koch(iter=1, niveau=niveau, taille=taille, delta=delta)
elif iter <= niveau: # Trace une section _/\_ du flocon
koch(iter=iter + 1, niveau=niveau, taille=taille, delta=delta)
T.left(60 + delta)
koch(iter=iter + 1, niveau=niveau, taille=taille, delta=delta)
T.right(120 + 2 * delta)
koch(iter=iter + 1, niveau=niveau, taille=taille, delta=delta)
T.left(60 + delta)
koch(iter=iter + 1, niveau=niveau, taille=taille, delta=delta)
else: # Trace le segment de dernier niveau
T.forward(taille / 3 ** (niveau + 1))
if __name__ == '__main__':
# start-argparse
# Exemple d'utilisation de la bibliothèque de gestion d'arguments 'argparse'
import argparse
desc = u"Tracé (via 'turtle') d'un flocon de Koch d'ordre arbitraire."
# Définition des options
parser = argparse.ArgumentParser(description=desc)
parser.add_argument('ordre', nargs='?', type=int,
help="Ordre du flocon, >0 [%(default)s]",
default=3)
parser.add_argument('-t', '--taille', type=int,
help="Taille de la figure, >0 [%(default)s px]",
default=500)
parser.add_argument('-d', '--delta', type=float,
help="Delta [%(default)s deg]",
default=0.)
parser.add_argument('-f', '--figure', type=str,
help="Nom de la figure de sortie (format EPS)")
parser.add_argument('-T', '--turbo',
action="store_true", default=False,
help="Mode Turbo")
# Déchiffrage des options et arguments
args = parser.parse_args()
# Quelques tests sur les args et options
if not args.ordre > 0:
parser.error("Ordre requis '{}' invalide".format(args.ordre))
if not args.taille > 0:
parser.error("La taille de la figure doit être positive")
# end-argparse
if args.turbo:
T.hideturtle()
T.speed(0)
# Tracé du flocon de Koch de niveau 3
koch(niveau=args.ordre, taille=args.taille, delta=args.delta)
if args.figure:
# Sauvegarde de l'image
print "Sauvegarde de la figure dans '{}'".format(args.figure)
T.getscreen().getcanvas().postscript(file=args.figure)
T.exitonclick()
Source : koch.py
X-H. Jeu du plus ou moins▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import random
nmin, nmax = 1, 100
nsol = random.randint(nmin, nmax)
print "Vous devez deviner un nombre entre {} et {}.".format(nmin, nmax)
ncoups = 0
try:
while True:
proposition = raw_input("Votre proposition: ")
try:
ntest = int(proposition)
if not nmin <= ntest <= nmax:
raise ValueError("Proposition invalide")
except ValueError:
print "Votre proposition {!r} n'est pas un entier " \
"compris entre {} et {}.".format(proposition, nmin, nmax)
continue
ncoups += 1
if nsol > ntest:
print "C'est plus."
elif nsol < ntest:
print "C'est moins."
else:
print "Vous avez trouvé en {} coup{}!".format(
ncoups, 's' if ncoups > 1 else '')
break # Interrompt la boucle while
except (KeyboardInterrupt, EOFError): # Interception de Ctrl-C et Ctrl-D
print "\nVous abandonnez après seulement {} coup{}!".format(
ncoups, 's' if ncoups > 1 else '')
Source : pm.py
X-I. Animaux▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
159.
160.
161.
162.
163.
164.
165.
166.
167.
168.
169.
170.
171.
172.
173.
174.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import pytest # Module (non-- standard) de tests
class Animal(object): # *object* est la classe dont dérivent toutes les autres
"""
Classe définissant un `Animal`, caractérisé par son nom et son
poids.
"""
def __init__(self, nom, masse):
"""
Méthode d'instanciation à partir d'un nom (str) et d'un poids (float).
"""
# Ici, convertir les paramètres pour être sûr qu'il ont le bon
# type. On utilisera `str` et `float`
self.nom = str(nom)
self.masse = float(masse)
self.vivant = True # Les animaux sont vivants à l'instanciation
self.empoisonne = False # Animal empoisonné ?
def __str__(self):
"""
Surcharge de l'opérateur `str`: l'affichage *informel* de l'objet
dans l'interpréteur, p.ex. `print self` sera résolu comme
`self.__str__()`
Retourne une chaîne de caractères.
"""
return "{a.nom} ({a.masse:.1f} kg)".format(a=self)
def estVivant(self):
"""Méthode booléenne, vraie si l'animal est vivant."""
return self.vivant
def mourir(self):
"""Change l'état interne de l'objet (ne retourne rien)."""
self.vivant = False
def __cmp__(self, other):
"""
Surcharge des opérateurs de comparaison, sur la base de la masse
des animaux.
"""
return cmp(self.masse, other.masse)
def __call__(self, other):
"""
Surcharge de l'opérateur '()' pour manger un autre animal (qui
meurt s'il est vivant) et prendre du poids (mais pas plus que
la masse de l'autre ou 10 % de son propre poids). Attention aux
animaux empoisonnés !
L'instruction `self(other)` sera résolue comme
`self.__call__(other).
"""
other.mourir()
poids = min(other.masse, self.masse * 0.1)
self.masse += poids
other.masse -= poids
if other.empoisonne:
self.mourir()
class Chien(Animal):
"""
Un `Chien` hérite de `Animal` avec des méthodes additionnelles
(p.ex. l'aboiement et l'odorat).
"""
def __init__(self, nom, masse=20, odorat=0.5):
"""Définit un chien plus ou moins fin limier."""
# Initialisation de la classe parente
Animal.__init__(self, nom, masse)
# Attribut propre à la classe dérivée
self.odorat = float(odorat)
def __str__(self):
return "{a.nom} (Chien, {a.masse:.1f} kg)".format(a=self)
def aboyer(self):
"""Une méthode bien spécifique aux chiens."""
print("Ouaf ! Ouaf !")
def estVivant(self):
"""Quand on vérifie qu'un chien est vivant, il aboie."""
vivant = Animal.estVivant(self)
if vivant:
self.aboyer()
return vivant
# start-tests
def test_empty_init():
with pytest.raises(TypeError):
Animal()
def test_wrong_init():
with pytest.raises(ValueError):
Animal('Youki', 'lalala')
def test_init():
youki = Animal('Youki', 600)
assert youki.masse == 600
assert youki.vivant
assert youki.estVivant()
assert not youki.empoisonne
# end-tests
def test_str():
youki = Animal('Youki', 600)
assert str(youki) == 'Youki (600.0 kg)'
def test_mort():
youki = Animal('Youki', 600)
assert youki.estVivant()
youki.mourir()
assert not youki.estVivant()
def test_lt():
medor = Animal('Medor', 600)
kiki = Animal('Kiki', 20)
assert kiki < medor
with pytest.raises(AttributeError):
medor < 1
def test_mange():
medor = Animal('Medor', 600)
kiki = Animal('Kiki', 20)
medor(kiki) # Médor mange Kiki
assert medor.estVivant()
assert not kiki.estVivant()
assert kiki.masse == 0
assert medor.masse == 620
kiki = Animal("Kiki Jr.", 20)
kiki(medor) # Kiki Jr. mange Médor
assert not medor.estVivant()
assert kiki.estVivant()
assert kiki.masse == 22
assert medor.masse == 618 # Médor a perdu du poids en se faisant manger!
def test_init_chien():
medor = Chien('Medor', 600)
assert isinstance(medor, Animal)
assert isinstance(medor, Chien)
assert medor.odorat == 0.5
assert str(medor) == 'Medor (Chien, 600.0 kg)'
assert medor.estVivant()
=========================== test session starts ============================
platform linux2 -- Python 2.7.6 -- py-1.4.24 -- pytest-2.6.2
collected 8 items
animauxSol.py ........
========================= 8 passed in 0.04 seconds =========================Source : animauxSol.py
X-J. Particules▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
159.
160.
161.
162.
163.
164.
165.
166.
167.
168.
169.
170.
171.
172.
173.
174.
175.
176.
177.
178.
179.
180.
181.
182.
183.
184.
185.
186.
187.
188.
189.
190.
191.
192.
193.
194.
195.
196.
197.
198.
199.
200.
201.
202.
203.
204.
205.
206.
207.
208.
209.
210.
211.
212.
213.
214.
215.
216.
217.
218.
219.
220.
221.
222.
223.
224.
225.
226.
227.
228.
229.
230.
231.
232.
233.
234.
235.
236.
237.
238.
239.
240.
241.
242.
243.
244.
245.
246.
247.
248.
249.
250.
251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
261.
262.
263.
264.
265.
266.
267.
268.
269.
270.
271.
272.
273.
274.
275.
276.
277.
278.
279.
280.
281.
282.
283.
284.
285.
286.
287.
288.
289.
290.
291.
292.
293.
294.
295.
296.
297.
298.
299.
300.
301.
302.
303.
304.
305.
306.
307.
308.
309.
310.
311.
312.
313.
314.
315.
316.
317.
318.
319.
320.
321.
322.
323.
324.
325.
326.
327.
328.
329.
330.
331.
332.
333.
334.
335.
336.
337.
338.
339.
340.
341.
342.
343.
344.
345.
346.
347.
348.
349.
350.
351.
352.
353.
354.
355.
356.
357.
358.
359.
360.
361.
362.
363.
364.
365.
366.
367.
368.
369.
370.
371.
372.
373.
374.
375.
376.
377.
378.
379.
380.
381.
382.
383.
384.
385.
386.
387.
388.
389.
390.
391.
392.
393.
394.
395.
396.
397.
398.
399.
400.
401.
402.
403.
404.
405.
406.
407.
408.
409.
410.
411.
412.
413.
414.
415.
416.
417.
418.
419.
420.
421.
422.
423.
424.
425.
426.
427.
428.
429.
430.
431.
432.
433.
434.
435.
436.
437.
438.
439.
440.
441.
442.
443.
444.
445.
446.
447.
448.
449.
450.
451.
452.
453.
454.
455.
456.
457.
458.
459.
460.
461.
462.
463.
464.
465.
466.
467.
468.
469.
470.
471.
472.
473.
474.
475.
476.
477.
478.
479.
480.
481.
482.
483.
484.
485.
486.
487.
488.
489.
490.
491.
492.
493.
494.
495.
496.
497.
498.
499.
500.
501.
502.
503.
504.
505.
506.
507.
508.
509.
510.
511.
512.
513.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2014-09-04 16:56:47 alicari>
from __future__ import division # division réelle de type python 3, admis
import pytest # pytest importé pour les tests unitaires
import math
"""
Définition d'une classe point matériel, avec sa masse,
sa position et sa vitesse, et des méthodes pour le déplacer.
Le main test applique cela à un problème à force centrale
gravitationnel ou électrostatique.
Remarque : toutes les unités ont été choisies adimensionnées.
"""
__author__ = "Adrien Licari <adrien.licari@ens-lyon.fr>"
# Un critère pour déterminer l'égalité entre réels
tolerance = 1e-8
#############################################################################
### Définition de la classe Vector, utile pour la position et la vitesse. ###
#############################################################################
class Vector(object):
"""
Une classe structure simple contenant 3 coordonnées.
Une méthode est disponible pour en calculer la norme et
une surcharge des opérateurs ==, !=, +, - et * est proposée.
"""
def __init__(self, x=0, y=0, z=0):
"""
Constructeur de la classe vector.
Par défaut, construit le vecteur nul.
Args:
x,y,z(float): Les composantes du vecteur à construire.
Raises:
TypeError en cas de composantes non réelles
"""
try:
self.x = float(x)
self.y = float(y)
self.z = float(z)
except (ValueError, TypeError, AttributeError):
raise TypeError("The given coordinates must be numbers")
def __str__(self):
"""
Surcharge de l'opérateur `str`.
Returns :
"(x,y,z)" with 2 decimals
"""
return "({:.2f},{:.2f},{:.2f})".format(self.x, self.y, self.z)
def __eq__(self, other):
"""
Surcharge de l'opérateur `==` pour tester l'égalité
entre deux vecteurs.
Args :
other(Vector): Un autre vecteur
Raises :
TypeError si other n'est pas un objet Vector
"""
try:
return abs(self.x - other.x) < tolerance and \
abs(self.y - other.y) < tolerance and \
abs(self.z - other.z) < tolerance
except (ValueError, TypeError, AttributeError):
raise TypeError("Tried to compare Vector and non-Vector objects")
def __ne__(self, other):
"""
Surcharge de l'opérateur `!=` pour tester l'inégalité
entre deux vecteurs.
Args :
other(Vector): Un autre vecteur
Raises :
TypeError si other n'est pas un objet Vector
"""
return not self == other
def __add__(self, other):
"""
Surcharge de l'opérateur `+` pour les vecteurs.
Args :
other(Vector): Un autre vecteur
Raises :
TypeError si other n'est pas un objet Vector
"""
try:
return Vector(self.x + other.x, self.y + other.y, self.z + other.z)
except (ValueError, TypeError, AttributeError):
raise TypeError("Tried to add Vector and non-Vector objects")
def __sub__(self, other):
"""
Surcharge de l'opérateur `-` pour les vecteurs.
Args :
other(Vector): Un autre vecteur
Raises :
TypeError si other n'est pas un objet Vector
"""
try:
return Vector(self.x - other.x, self.y - other.y, self.z - other.z)
except (ValueError, TypeError, AttributeError):
raise TypeError("Tried to substract Vector and non-Vector objects")
def __mul__(self, number):
"""
Surcharge de l'opérateur `*` pour la multiplication entre
un vecteur et un nombre.
Args :
number(float): Un nombre à multiplier par le Vector.
Raises :
TypeError si other n'est pas un nombre
"""
try:
return Vector(number * self.x, number * self.y, number * self.z)
except (ValueError, TypeError, AttributeError):
raise TypeError("Tried to multiply Vector and non-number objects")
__rmul__ = __mul__ # Ligne pour autoriser la multiplication à droite
def norm(self):
"""
Calcul de la norme 2 d'un vecteur.
Returns :
sqrt(x**2 + y**2 + z**2)
"""
return (self.x ** 2 + self.y ** 2 + self.z ** 2) ** (1 / 2)
def clone(self):
"""
Méthode pour construire un nouveau Vecteur, copie de self.
"""
return Vector(self.x, self.y, self.z)
###############################################
##### Quelques test pour la classe Vector #####
###############################################
def test_VectorInit():
with pytest.raises(TypeError):
vec = Vector('Test', 'avec', 'strings')
vec = Vector(Vector())
vec = Vector([])
vec = Vector(0, -53.76, math.pi)
assert vec.x == 0
assert vec.y == -53.76
assert vec.z == math.pi
def test_VectorStr():
vec = Vector(0, 600, -2)
assert str(vec) == '(0.00,600.00,-2.00)'
def test_VectorEq(): # teste aussi l'opérateur !=
vec = Vector(2, 3, -5)
vec2 = Vector(2, 3, -4)
assert vec != vec2
assert vec != Vector(0, 3, -5)
with pytest.raises(TypeError):
Vector(2, 1, 4) == "Testing strings"
Vector(2, 1, 4) == 42
Vector(2, 1, 4) == ['list']
def test_VectorAdd():
vec = Vector(2, 3, -5)
vec2 = Vector(2, -50, 5)
assert (vec + vec2) == Vector(4, -47, 0)
def test_VectorSub():
vec = Vector(1, -7, 9)
vec2 = Vector()
assert (vec - vec) == Vector()
assert (vec - vec2) == vec
def test_VectorMul():
vec = Vector(1, -7, 9) * 2
vec2 = 6 * Vector(1, -1, 2)
assert vec == Vector(2, -14, 18)
assert vec2 == Vector(6, -6, 12)
def test_VectorNorm():
assert Vector().norm() == 0
assert Vector(1, 0, 0).norm() == 1
assert Vector(2, -5, -4).norm() == 45 ** (1 / 2)
def test_VectorClone():
vec = Vector(3, 2, 9)
vec2 = vec.clone()
assert vec == vec2
vec2.x = 1
assert vec != vec2
############################################################
##### Une classe point matériel qui se gère en interne #####
############################################################
class Particle(object):
"""
La classe Particle représente un point matériel doté d'une masse,
d'une position et d'une vitesse. Elle possède également une méthode
pour calculer la force gravitationnelle exercée par une autre particule.
Enfin, la méthode update lui permet de mettre à jour sa position et
sa vitesse en fonction des forces subies.
"""
def __init__(self, mass=1, position=Vector(), speed=Vector()):
"""
Le constructeur de la classe Particle.
Définit un point matériel avec une position et une vitesse initiales.
Args :
mass(float): La masse de la particule (doit être
strictement positive)
position(Vector): La position initiale de la particule
speed(Vector): La vitesse initiale de la particule
Raises :
TypeError si la masse n'est pas un nombre, ou si la position ou
la vitesse ne sont pas des Vector
ValueError si la masse est négative ou nulle
"""
try:
self.mass = float(mass)
self.position = position.clone()
self.speed = speed.clone()
except (ValueError, TypeError, AttributeError):
raise TypeError("The mass must be a positive float number. "
"The position and speed must Vector objects.")
try:
assert mass > 0 # une masse négative ou nulle pose des problèmes
except AssertionError:
raise ValueError("The mass must be strictly positive")
self.force = Vector()
def __str__(self):
"""
Surcharge de l'opérateur `str`.
Returns :
"Particle with mass m, position (x,y,z) and speed (vx,vy,vz)"
with 2 decimals
"""
return "Particle with mass {:.2f}, position {} " \
"and speed {}".format(self.mass, self.position, self.speed)
def computeForce(self, other):
"""
Calcule la force gravitationnelle exercée par une Particule
other sur self.
Args :
other(Particle): Une autre particule, source de l'interaction
Raises :
TypeError si other n'est pas un objet Vector
"""
try:
r = self.position - other.position
self.force = -self.mass * other.mass / r.norm() ** 3 * r
except AttributeError:
raise TypeError("Tried to compute the force created by "
"a non-Particle object")
def update(self, dt):
"""
Mise à jour de la position et la vitesse au cours du temps.
Args :
dt(float): Pas de temps d'intégration.
"""
try:
d = float(dt)
except (ValueError, TypeError, AttributeError):
raise TypeError("The integration timestep must be a number")
self.speed += self.force * dt * (1 / self.mass)
self.position += self.speed * dt
#############################################
##### Des tests pour la classe Particle #####
#############################################
def test_ParticleInit():
with pytest.raises(TypeError):
p = Particle("blabla")
p = Particle(2, position='hum') # on vérifie les erreurs sur Vector
p = Particle([])
p = Particle(3, Vector(2, 1, 4), Vector(-1, -1, -1))
assert p.mass == 3
assert p.position == Vector(2, 1, 4)
assert p.speed == Vector(-1, -1, -1)
assert p.force == Vector()
def test_ParticleStr():
p = Particle(3, Vector(1, 2, 3), Vector(-1, -2, -3))
assert str(p) == "Particle with mass 3.00, position (1.00,2.00,3.00) " \
"and speed (-1.00,-2.00,-3.00)"
def test_ParticleForce():
p = Particle(1, Vector(1, 0, 0))
p2 = Particle()
p.computeForce(p2)
assert p.force == Vector(-1, 0, 0)
p.position = Vector(2, -3, 6)
p.mass = 49
p.computeForce(p2)
assert p.force == Vector(-2 / 7, 3 / 7, -6 / 7)
def test_ParticleUpdate():
dt = 0.1
p = Particle(1, Vector(1, 0, 0), Vector())
p.computeForce(Particle())
p.update(dt)
assert p.speed == Vector(-0.1, 0, 0)
assert p.position == Vector(0.99, 0, 0)
#######################################################
##### Une classe Ion qui hérite de point matériel #####
#######################################################
class Ion (Particle):
"""
Un Ion est une particule ayant une charge en plus de sa masse et
intéragissant électrostatiquement plutôt que gravitationnellement.
La méthode computeForce remplace donc le calcul de la force
gravitationnelle de Newton par celui de la force
électrostatique de Coulomb.
"""
def __init__(self, mass=1, charge=1, position=Vector(), speed=Vector()):
"""
Le constructeur de la classe Ion.
Args :
mass(float): La masse de l'ion (doit être strictement positive)
charge(float): La charge de l'ion (doit être entière et
strictement positive)
position(Vector): La position initiale de la particule
speed(Vector): La vitesse initiale de la particule
Raises :
ValueError si charge < 0
TypeError si la masse n'est pas un réel,
si la charge n'est pas un entier,
si position ou speed ne sont pas des Vector
"""
Particle.__init__(self, mass, position, speed)
try:
self.charge = int(charge)
except (ValueError, AttributeError, TypeError):
raise TypeError("The charge must be an integer.")
try:
assert self.charge > 0
except AssertionError:
raise ValueError("The charge must be positive.")
def __str__(self):
"""
Surcharge de l'opérateur `str`.
Returns :
"Ion with mass m, charge q, position (x,y,z)
and speed (vx,vy,vz)" avec q entier et le reste à 2 décimales
"""
return "Ion with mass {:.2f}, charge {:d}, position {} " \
"and speed {}".format(self.mass, self.charge,
self.position, self.speed)
def computeForce(self, other):
"""
Calcule la force électrostatique de Coulomb exercée par un Ion other
sur self. Masque la méthode de Particle.
Args :
other(Ion): Un autre Ion, source de l'interaction.
Raises :
TypeError si other n'est pas un objet Ion
"""
try:
r = self.position - other.position
self.force = self.charge * other.charge / r.norm() ** 3 * r
except (AttributeError, TypeError, ValueError):
raise TypeError("Tried to compute the force created by "
"a non-Ion object")
#######################################
##### Des test pour la classe Ion #####
#######################################
def test_IonInit():
with pytest.raises(TypeError):
ion = Ion("blabla")
ion = Ion(2, position='hum') # on vérifie une erreur sur Vector
ion = Ion(2, 'hum') # on vérifie une erreur sur la charge
ion = Ion(2, 3, Vector(2, 1, 4), Vector(-1, -1, -1))
assert ion.mass == 2
assert ion.charge == 3
assert ion.position == Vector(2, 1, 4)
assert ion.speed == Vector(-1, -1, -1)
assert ion.force == Vector()
def test_IonStr():
ion = Ion(3, 2, Vector(1, 2, 3), Vector(-1, -2, -3))
assert str(ion) == "Ion with mass 3.00, charge 2, " \
"position (1.00,2.00,3.00) and speed (-1.00,-2.00,-3.00)"
def test_IonForce():
ion = Ion(mass=1, charge=1, position=Vector(1, 0, 0))
ion2 = Ion(charge=3)
ion.computeForce(ion2)
assert ion.force == Vector(3, 0, 0)
ion = Ion(charge=49, position=Vector(2, -3, 6))
ion.computeForce(ion2)
assert ion.force == Vector(6 / 7, -9 / 7, 18 / 7)
###########################
##### Un main de test #####
###########################
if __name__ == '__main__':
# On lance tous les tests en bloc pour commencer
print " Test functions ".center(50, "*")
print "Testing Vector class...",
test_VectorInit()
test_VectorStr()
test_VectorEq()
test_VectorAdd()
test_VectorSub()
test_VectorMul()
test_VectorNorm()
test_VectorClone()
print "ok"
print "Testing Particle class...",
test_ParticleInit()
test_ParticleStr()
test_ParticleForce()
test_ParticleUpdate()
print "ok"
print "Testing Ion class...",
test_IonInit()
test_IonStr()
test_IonForce()
print "ok"
print " Test end ".center(50, "*"), "\n"
# Un petit calcul physique
print " Physical computations ".center(50, "*")
dt = 0.0001
# problème à force centrale gravitationnelles, cas circulaire
ntimesteps = int(10000 * math.pi) # durée pour parcourir pi
center = Particle()
M = Particle(mass=1, position=Vector(1, 0, 0), speed=Vector(0, 1, 0))
print "** Gravitationnal computation of central-force motion for a {}" \
.format(str(M))
for i in range(ntimesteps):
M.computeForce(center)
M.update(dt)
print "\t => Final system : {}".format(str(M))
# problème à force centrale électrostatique, cas rectiligne
center = Ion()
M = Ion(charge=4, position=Vector(0, 0, 1), speed=Vector(0, 0, -1))
print "** Electrostatic computation of central-force motion for a {}" \
.format(str(M))
for i in range(ntimesteps):
M.computeForce(center)
M.update(dt)
print "\t => Final system : {}".format(str(M))
print " Physical computations end ".center(50, "*")
Source : particleSol.py
X-K. Jeu de la vie▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2017-07-09 19:14 ycopin@lyonovae03.in2p3.fr>
import random
class Life(object):
cells = {False: ".", True: "#"} # Dead and living cell representations
def __init__(self, h, w, periodic=False):
"""
Create a 2D-list (the game grid *G*) with the wanted size (*h*
rows, *w* columns) and initialize it with random booleans
(dead/alive). The world is periodic if *periodic* is True.
"""
self.h = int(h)
self.w = int(w)
assert self.h > 0 and self.w > 0
# Random initialization of a h×w world
self.world = [[random.choice([True, False])
for j in range(self.w)]
for i in range(self.h)] # h rows of w elements
self.periodic = periodic
def get(self, i, j):
"""
This method returns the state of cell (*i*,*j*) safely, even
if the (*i*,*j*) is outside the grid.
"""
if self.periodic:
return self.world[i % self.h][j % self.w] # Periodic conditions
else:
if (0 <= i < self.h) and (0 <= j < self.w): # Inside grid
return self.world[i][j]
else: # Outside grid
return False # There's nobody out there...
def __str__(self):
"""
Convert the grid to a visually handy string.
"""
return '\n'.join([''.join([self.cells[val] for val in row])
for row in self.world])
def evolve_cell(self, i, j):
"""
Tells if cell (*i*,*j*) will survive during game iteration,
depending on the number of living neighboring cells.
"""
alive = self.get(i, j) # Current cell status
# Count living cells *around* current one (excluding current one)
count = sum(self.get(i + ii, j + jj)
for ii in [-1, 0, 1]
for jj in [-1, 0, 1]
if (ii, jj) != (0, 0))
if count == 3:
# A cell w/ 3 neighbors will either stay alive or resuscitate
future = True
elif count < 2 or count > 3:
# A cell w/ too few or too many neighbors will die
future = False
else:
# A cell w/ 2 or 3 neighbors will stay as it is (dead or alive)
future = alive # Current status
return future
def evolve(self):
"""
Evolve the game grid by one step.
"""
# Update the grid
self.world = [[self.evolve_cell(i, j)
for j in range(self.w)]
for i in range(self.h)]
if __name__ == "__main__":
import time
h, w = (20, 60) # (nrows,ncolumns)
# Instanciation (including initialization)
life = Life(h, w, periodic=True)
while True: # Infinite loop! (Ctrl-C to break)
print life # Print current world
print "\n"
time.sleep(0.1) # Pause a bit
life.evolve() # Evolve world
Source : life.py
X-L. Median Absolute Deviation▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as N
def mad(a, axis=None):
"""
Compute *Median Absolute Deviation* of an array along given axis.
"""
# Median along given axis, but *keeping* the reduced axis so that
# result can still broadcast against a.
med = N.median(a, axis=axis, keepdims=True)
mad = N.median(N.absolute(a - med), axis=axis) # MAD along given axis
return mad
if __name__ == '__main__':
x = N.arange(4 * 5, dtype=float).reshape(4, 5)
print "x =\n", x
print "MAD(x, axis=None) =", mad(x)
print "MAD(x, axis=0) =", mad(x, axis=0)
print "MAD(x, axis=1) =", mad(x, axis=1)
print "MAD(x, axis=(0, 1)) =", mad(x, axis=(0, 1))
Source : mad.py
X-M. Distribution du pull▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as N
def pull(x, dx):
"""
Compute the pull from x, dx.
* Input data: x = [x_i], error dx = [s_i] Optimal
* (variance-weighted) mean: E = sum(x_i/s_i²)/sum(1/s_i²) Variance
* on weighted mean: var(E) = 1/sum(1/s_i²) Pull: p_i = (x_i -
* E_i)/sqrt(var(E_i) + s_i²) where E_i and var(E_i) are computed
* without point i.
If errors s_i are correct, the pull distribution is centered on 0
with standard deviation of 1.
"""
assert x.ndim == dx.ndim == 1, "pull works on 1D-arrays only."
assert len(x) == len(dx), "dx should be the same length as x."
n = len(x)
i = N.resize(N.arange(n), n * n) # 0,...,n-1,0,...n-1,..., n times (n²,)
i[::n + 1] = -1 # Mark successively 0,1,2,...,n-1
# Remove marked indices & reshape (n,n-1)
j = i[i >= 0].reshape((n, n - 1))
v = dx ** 2 # Variance
w = 1 / v # Variance (optimal) weighting
Ei = N.average(x[j], weights=w[j], axis=1) # Weighted mean (n,)
vEi = 1 / N.sum(w[j], axis=1) # Variance of mean (n,)
p = (x - Ei) / N.sqrt(vEi + v) # Pull (n,)
return p
if __name__ == '__main__':
import matplotlib.pyplot as P
import scipy.stats as SS
n = 1000
mu = 1.
sig = 2.
# Normally distributed random sample of size n, with mean=mu and std=sig
x = N.random.normal(loc=mu, scale=sig, size=n)
dx = N.full_like(x, sig) # Formal (true) errors
p = pull(x, dx) # Pull computation
m, s = p.mean(), p.std(ddof=1)
print "Pull ({} entries): mean={:.2f}, std={:.2f}".format(n, m, s)
fig, ax = P.subplots()
_, bins, _ = ax.hist(p, bins='auto', normed=True,
histtype='stepfilled',
label=u"#={}, µ={:.3f}, σ={:.3f}".format(n, m, s))
y = N.linspace(-3, 3)
ax.plot(y, SS.norm.pdf(y), label=ur"$\mathcal{N}$(µ=0, σ²=1)")
ax.set(title='Pull distribution', xlabel='Pull')
ax.legend(loc='upper left')
P.show()
Source : pull.py
X-N. Calculs numériques (numerique.ipynb)▲
import numpy as N
import matplotlib.pyplot as P
# Insert figures within notebook
%matplotlib inlineX-N-1. Quadrature▲
Calcul de l'intégrale
|
kitxmlcodeinlinelatexdvp\int_0^\infty \frac{x^3}{e^x - 1}\mathrm{d}x = \frac{\pi^4}{15}finkitxmlcodeinlinelatexdvp |
In [3] :import scipy.integrate as SI
def integrand(x):
return x**3 / (N.exp(x) - 1)q, dq = SI.quad(integrand, 0, N.inf)
print "Intégrale:", q
print "Erreur estimée:", dq
print "Erreur absolue:", (q - (N.pi ** 4 / 15))Intégrale : 6.49393940227
Erreur estimée : 2.62847076684e-09
Erreur absolue : 1.7763568394e-15
/data/ycopin/Softs/local/lib/python2.7/site-packages/ipykernel/__main__.py:3: RuntimeWarning: overflow encountered in exp
app.launch_new_instance()X-N-2. Zéro d'une fonction▲
Résolution numérique de l'équation
kitxmlcodelatexdvpf(x) = \frac{x\,e^x}{e^x - 1} - 5 = 0finkitxmlcodelatexdvpdef func(x):
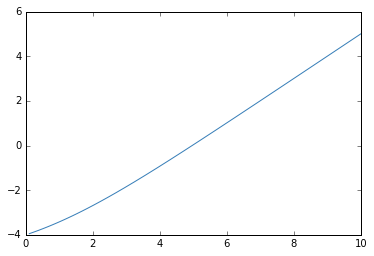
return x * N.exp(x) / (N.exp(x) - 1) - 5Il faut d'abord déterminer un intervalle contenant la solution, c.-à-d. le zéro de func. Puisque kitxmlcodeinlinelatexdvpf(0^+) = -4 < 0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpf(10) \simeq 5 > 0finkitxmlcodeinlinelatexdvp, il est intéressant de tracer l'allure de la courbe sur ce domaine :
x = N.logspace(-1, 1) # 50 points logarithmiquement espacés de 10**-1 = 0.1 à 10**1 = 10
P.plot(x, func(x));|
|
In [7] :import scipy.optimize as SO
zero = SO.brentq(func, 1, 10)
print "Solution:", zeroSolution : 4.96511423174
X-O. Quartet d'Anscombe▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as N
import scipy.stats as SS
import matplotlib.pyplot as P
def printStats(x, y):
"""
Print out means and variances for x and y, as well as correlation
coeff. (Pearson) and linear regression for y vs. x.
"""
assert N.shape(x) == N.shape(y), "Incompatible input arrays"
print "x: mean={:.2f}, variance={:.2f}".format(N.mean(x), N.var(x))
print "y: mean={:.2f}, variance={:.2f}".format(N.mean(y), N.var(y))
print "y vs. x: corrcoeff={:.2f}".format(SS.pearsonr(x, y)[0])
# slope, intercept, r_value, p_value, std_err
a, b, _, _, _ = SS.linregress(x, y)
print "y vs. x: y = {:.2f} x + {:.2f}".format(a, b)
def plotStats(ax, x, y, title='', fancy=True):
"""
Plot y vs. x, and linear regression.
"""
assert N.shape(x) == N.shape(y), "Incompatible input arrays"
# slope, intercept, r_value, p_value, std_err
a, b, r, _, _ = SS.linregress(x, y)
# Data + corrcoeff
ax.plot(x, y, 'bo', label="r = {:.2f}".format(r))
# Linear regression
xx = N.array([0, 20])
yy = a * xx + b
ax.plot(xx, yy, 'r-', label="y = {:.2f} x + {:.2f}".format(a, b))
leg = ax.legend(loc='upper left', fontsize='small')
if fancy: # Additional stuff
# Add mean line ± stddev
m = N.mean(x)
s = N.std(x, ddof=1)
ax.axvline(m, color='g', ls='--', label='_') # Mean
ax.axvspan(m - s, m + s, color='g', alpha=0.2, label='_') # Std-dev
m = N.mean(y)
s = N.std(y, ddof=1)
ax.axhline(m, color='g', ls='--', label='_') # Mean
ax.axhspan(m - s, m + s, color='g', alpha=0.2, label='_') # Std-dev
# Title and labels
ax.set_title(title)
if ax.is_last_row():
ax.set_xlabel("x")
if ax.is_first_col():
ax.set_ylabel("y")
if __name__ == '__main__':
quartet = N.genfromtxt("anscombe.dat") # Read Anscombe's Quartet
fig = P.figure()
for i in range(4): # Loop over quartet sets x,y
ax = fig.add_subplot(2, 2, i + 1)
print "Dataset #{} ".format(i + 1) + "=" * 20
x, y = quartet[:, 2 * i:2 * i + 2].T
printStats(x, y) # Print main statistics
plotStats(ax, x, y, title=str(i + 1)) # Plots
fig.suptitle("Anscombe's Quartet", fontsize='x-large')
P.show()
$ python anscombe.py
Dataset 1 ====================
x: mean=9.00, variance=10.00
y: mean=7.50, variance=3.75
y vs. x: corrcoeff=0.82
y vs. x: y = 0.50 x + 3.00
Dataset 2 ====================
x: mean=9.00, variance=10.00
y: mean=7.50, variance=3.75
y vs. x: corrcoeff=0.82
y vs. x: y = 0.50 x + 3.00
Dataset 3 ====================
x: mean=9.00, variance=10.00
y: mean=7.50, variance=3.75
y vs. x: corrcoeff=0.82
y vs. x: y = 0.50 x + 3.00
Dataset 4 ====================
x: mean=9.00, variance=10.00
y: mean=7.50, variance=3.75
y vs. x: corrcoeff=0.82
y vs. x: y = 0.50 x + 3.00Source : anscombe.py
X-P. Suite logistique▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2012-09-05 02:37 ycopin@lyopc469>
import numpy as np
import random
import matplotlib.pyplot as plt
def iteration(r, niter=100):
x = random.uniform(0, 1)
i = 0
while i < niter and x < 1:
x = r * x * (1 - x)
i += 1
return x if x < 1 else -1
def generate_diagram(r, ntrials=50):
"""
Cette fonction retourne (jusqu'à) *ntrials* valeurs d'équilibre
pour les *r* d'entrée. Elle renvoie un tuple :
+ le premier élément est la liste des valeurs prises par le paramètre *r*
+ le second est la liste des points d'équilibre correspondants
"""
r_v = []
x_v = []
for rr in r:
j = 0
while j < ntrials:
xx = iteration(rr)
if xx > 0: # Convergence : il s'agit d'une valeur d'équilibre
r_v.append(rr)
x_v.append(xx)
j += 1 # Nouvel essai
return r_v, x_v
r = np.linspace(0, 4, 1000)
x, y = generate_diagram(r)
plt.plot(x, y, 'r,')
plt.xlabel('r')
plt.ylabel('x')
plt.show()
Source : logistique.py
X-Q. Ensemble de Julia▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2012-09-05 02:10 ycopin@lyopc469>
"""Visualisation de l'ensemble de julia
<http://fr.wikipedia.org/wiki/Ensemble_de_Julia>`_.
Exercice: proposer des solutions pour accélérer le calcul.
"""
import numpy as np
import matplotlib.pyplot as plt
c = complex(0.284, 0.0122) # Constante
xlim = 1.5 # [-xlim,xlim] × i[-xlim,xlim]
nx = 1000 # Nb de pixels
niter = 100 # Nb d'itérations
x = np.linspace(-xlim, xlim, nx) # nx valeurs de -xlim à +xlim
xx, yy = np.meshgrid(x, x) # Tableaux 2D
z = xx + 1j * yy # Portion du plan complexe
for i in range(niter): # Itération: z(n+1) = z(n)**2 + c
z = z ** 2 + c
# Visualisation
plt.imshow(np.abs(z), extent=[-xlim, xlim, -xlim, xlim], aspect='equal')
plt.title(c)
plt.show()
Source : julia.py
X-R. Trajectoire d'un boulet de canon (canon.ipynb)▲
Nous allons intégrer les équations du mouvement pour un boulet de canon soumis à des forces de frottement « turbulentes » (non linéaires) :
|
kitxmlcodeinlinelatexdvp\ddot{\mathbf{r}} = \mathbf{g} - \frac{\alpha}{m}v\times\mathbf{v}.finkitxmlcodeinlinelatexdvp |
Cette équation différentielle non linéaire du 2d ordre doit être réécrite sous la forme de deux équations différentielles couplées du 1er ordre:
|
kitxmlcodeinlinelatexdvp\begin{split}\begin{cases} \dot{\mathbf{r}} &= \mathbf{v} \\ \dot{\mathbf{v}} &= \mathbf{g} - \frac{\alpha}{m}v\times\mathbf{v}. \end{cases}\end{split}finkitxmlcodeinlinelatexdvp |
Il s'agit donc de résoudre une seule équation différentielle du 1er ordre en kitxmlcodeinlinelatexdvp\mathbf{z} = (\mathbf{r},\mathbf{v})finkitxmlcodeinlinelatexdvp
In [1] :
2.
3.
4.
5.
%matplotlib inline
import numpy as N
import scipy.integrate as SI
import matplotlib.pyplot as P
Valeurs numériques pour un boulet de canon de 36 livres :
In [2] :
2.
3.
4.
5.
6.
7.
8.
9.
g = 9.81 # Pesanteur [m/s2]
cx = 0.45 # Coefficient de frottement d'une sphère
rhoAir = 1.2 # Masse volumique de l'air [kg/m3] au niveau de la mer, T=20°C
rad = 0.1748/2 # Rayon du boulet [m]
rho = 6.23e3 # Masse volumique du boulet [kg/m3]
mass = 4./3.*N.pi*rad**3 * rho # Masse du boulet [kg]
alpha = 0.5*cx*rhoAir*N.pi*rad**2 / mass # Coefficient de frottement par unité de masse
print "Masse du boulet: {:.2f} kg".format(mass)
print "Coefficient de frottement par unité de masse: {} S.I.".format(alpha)
Out [2] :
Masse du boulet : 17.42 kg
Coefficient de frottement par unité de masse : 0.000371899460424 S.I.Conditions initiales :
In [3] :
2.
3.
4.
v0 = 450. # Vitesse initiale [m/s]
alt = 45. # Inclinaison du canon [deg]
alt *= N.pi/180. # Inclinaison [rad]
z0 = (0.,0.,v0*N.cos(alt),v0*N.sin(alt)) # (x0,y0,vx0,vy0)
Temps caractéristique du système : kitxmlcodeinlinelatexdvpt = \sqrt{\frac{m}{g\alpha}}finkitxmlcodeinlinelatexdvp(durée du régime transitoire). L'intégration des équations se fera sur un temps caractéristique, avec des pas de temps significativement plus petits.
In [4] :
2.
3.
tc = N.sqrt(mass/(g * alpha))
print "Temps caractéristique: {:.1f} s".format(tc)
t = N.linspace(0, tc, 100)
Temps caractéristique : 69.1 s
Définition de la fonction kitxmlcodeinlinelatexdvp\dot{\mathbf{z}}finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvp\mathbf{z} = (\mathbf{r},\mathbf{v})finkitxmlcodeinlinelatexdvp
In [5] :
2.
3.
4.
5.
6.
7.
def zdot(z, t):
"""Calcul de la dérivée de z=(x,y,vx,vy) à l'instant t."""
x,y,vx,vy = z
alphav = alpha * N.hypot(vx, vy)
return (vx,vy,-alphav*vx,-g-alphav*vy) # dz/dt = (vx,vy,x..,y..)
Intégration numérique des équations du mouvement à l'aide de la fonction scipy.integrate.odeint :
In [6] : zs = SI.odeint(zdot, z0, t)
Le tableau zs contient les valeurs de kitxmlcodeinlinelatexdvpzfinkitxmlcodeinlinelatexdvpà chaque instantkitxmlcodeinlinelatexdvptfinkitxmlcodeinlinelatexdvp : il est donc de taille (len(t),4).
In [7] :
2.
3.
4.
5.
ypos = zs[:,1]>=0 # y>0?
print "temps de coll. t(y~0) = {:.0f} s".format(t[ypos][-1]) # Dernier instant pour lequel y>0
print "portée x(y~0) = {:.0f} m".format(zs[ypos,0][-1]) # Portée approximative du canon
#print "y(y~0) = {:.0f} m".format(zs[ypos,1][-1]) # ~0
print "vitesse(y~0): {:.0f} m/s".format(N.hypot(zs[ypos,2][-1],zs[ypos,3][-1]))
temps de coll. t(y~0) = 36 s
portée x(y~0) = 3966 m
vitesse(y~0): 140 m/sIn [8] :
2.
3.
4.
5.
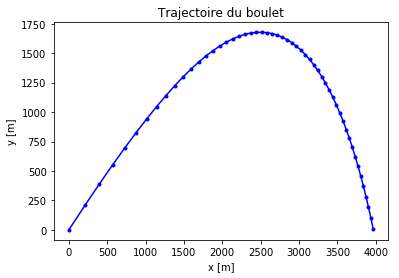
fig,ax = P.subplots()
ax.plot(zs[ypos,0],zs[ypos,1], 'b.-')
ax.set_xlabel("x [m]")
ax.set_ylabel("y [m]")
ax.set_title("Trajectoire du boulet")
Out[8] : <matplotlib.text.Text at 0x7fe8d8b06950>
|
|
XI. Note de la rédaction de Developpez.com▲
Nous tenons à remercier Yannick Copin qui nous a aimablement autorisés à publier son tutoriel : Analyse scientifique avec Python. Nous remercions également Claude Leloup pour la relecture orthographique.
L'auteur, Yannick Copin, est maître de conférences au sein de l'équipe Cosmologie observationnelle/EUCLID de l'Institut de Physique Nucléaire de Lyon de l'Université Claude Bernard (Lyon 1).