VIII. Exemples▲
VIII-A. Mean power (fonction, argparse)▲
Sélectionnez
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Exemple de script (shebang, docstring, etc.) permettant une
utilisation en module (`import mean_power`) et en exécutable (`python
mean_power.py -h`);
"""
from __future__ import division # Les divisions entre entiers ne sont pas euclidiennes
def mean_power(alist, power=1):
"""
Retourne la racine `power` de la moyenne des éléments de `alist` à
la puissance `power`:
.. math:: \mu = (\frac{1}{N}\sum_{i=0}^{N-1} x_i^p)^{1/p}
`power=1` correspond à la moyenne arithmétique, `power=2` au *Root
Mean Squared*, etc.
Exemples:
>>> mean_power([1, 2, 3])
2.0
>>> mean_power([1, 2, 3], power=2)
2.160246899469287
"""
s = 0. # Initialisation de la variable *s* comme *float*
for val in alist: # Boucle sur les éléments de *alist*
s += val ** power # *s* est augmenté de *val* puissance *power*
# *mean* = (somme valeurs / nb valeurs)**(1/power)
mean = (s / len(alist)) ** (1 / power) # ATTENTION aux divisions euclidiennes !
return mean
if __name__ == '__main__':
# start-argparse
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('list', nargs='*', type=float, metavar='nombres',
help="Liste de nombres à moyenner")
parser.add_argument('-i', '--input', nargs='?', type=file,
help="Fichier contenant les nombres à moyenner")
parser.add_argument('-p', '--power', type=float, default=1.,
help="'Puissance' de la moyenne (%default)")
args = parser.parse_args()
# end-argparse
if args.input: # Lecture des coordonnées du fichier d'entrée
# Le fichier a déjà été ouvert en lecture par argparse (type=file)
try:
args.list = [float(x) for x in args.input
if not x.strip().startswith('#')]
except ValueError:
parser.error(
"Impossible de déchiffrer la ligne '{}' du fichier '{}'".format(
x, args.input))
# Vérifie qu'il y a au moins un nombre dans la liste
if not args.list:
parser.error("La liste doit contenir au moins un nombre")
# Calcul
moyenne = mean_power(alist, args.power)
# Affichage du résultat
print "La moyenne des {} nombres à la puissance {} est {}".format(
len(alist), args.power, moyenne)
Source : mean_power.py
VIII-B. Formes (POO)▲
Sélectionnez
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Exemple de Programmation Orientée Objet.
"""
__author__ = "Mathieu Leocmach <mathieu.leocmach@ens-lyon.fr>"
__version__ = "Time-stamp: <2014-10-03 10:54 mathieu.leocmach@ens-lyon.fr>"
# Définition d'une classe ==============================
class Forme(object): # *object* est la classe dont dérivent toutes les autres
"""Une forme plane, avec éventuellement une couleur."""
def __init__(self, couleur=None):
"""Initialisation d'une Forme, sans couleur par défaut."""
if couleur is None:
self.couleur = 'indéfinie'
else:
self.couleur = couleur
def __str__(self):
"""
Surcharge de la fonction `str()`: l'affichage *informel* de
l'objet dans l'interpréteur, p.ex. `print a` sera résolu comme
`a.__str__()`
Retourne une chaîne de caractères.
"""
return "Forme encore indéfinie de couleur {}".format(self.couleur)
def change_couleur(self, newcolor):
"""Change la couleur de la Forme."""
self.couleur = newcolor
def aire(self):
"""
Renvoi l'aire de la Forme.
L'aire ne peut pas être calculée dans le cas où la forme n'est
pas encore spécifiée : c'est ce que l'on appelle une méthode
'abstraite', qui pourra être précisée dans les classes filles.
"""
raise NotImplementedError(
"Impossible de calculer l'aire d'une forme indéfinie.")
def __cmp__(self, other):
"""
Comparaison de deux Formes sur la base de leur aire.
Surcharge des opérateurs de comparaison de type `{self} <
{other}`: la comparaison sera résolue comme
`self.__cmp__(other)` et le résultat sera correctement
interprété.
.. WARNING:: cette construction n'est plus supportée en Python3.
"""
return cmp(self.aire(), other.aire()) # Opérateur de comparaison
class Rectangle(Forme):
"""
Un Rectangle est une Forme particulière.
La classe fille hérite des attributs et méthodes de la
classe -mère, mais peut les surcharger (i.e. en changer la
définition), ou en ajouter de nouveaux:
- les méthodes `Rectangle.change_couleur()` et
`Rectangle.__cmp__()` dérivent directement de
`Forme.change_couleur()` et `Forme.__cmp__()`;
- `Rectangle.__str__()` surcharge `Forme.__str__()`;
- `Rectangle.aire()` définit la méthode jusqu'alors abstraite
`Forme.aire()`;
- `Rectangle.allonger()` est une nouvelle méthode propre à
`Rectangle`.
"""
def __init__(self, longueur, largeur, couleur=None):
"""
Initialisation d'un Rectangle longueur × largeur, sans couleur par
défaut.
"""
# Initialisation de la classe parente (nécessaire pour assurer
# l'héritage)
Forme.__init__(self, couleur)
# Attributs propres à la classe Rectangle
self.longueur = longueur
self.largeur = largeur
def __str__(self):
"""Surcharge de `Forme.__str__()`."""
return "Rectangle {}x{}, de couleur {}".format(
self.longueur, self.largeur, self.couleur)
def aire(self):
"""
Renvoie l'aire du Rectangle.
Cette méthode définit la méthode abstraite `Forme.area()`,
pour les Rectangles uniquement.
"""
return self.longueur * self.largeur
def allonger(self, facteur):
"""Multiplie la *longueur* du Rectangle par un facteur"""
self.longueur *= facteur
if __name__ == '__main__':
s = Forme() # Forme indéfinie et sans couleur
print "s:", str(s) # Interprété comme `s.__str__()`
s.change_couleur('rouge') # On change la couleur
print "s après change_couleur:", str(s)
try:
print "Aire de s:", s.aire() # La méthode abstraite lève une exception
except NotImplementedError as err:
print err
q = Rectangle(1, 4, 'vert') # Rectangle 1×4 vert
print "q:", str(q)
print "Aire de q:", q.aire()
r = Rectangle(2, 1, 'bleu') # Rectangle 2×1 bleu
print "r:", str(r)
print "Aire de r:", r.aire()
print "r >= q:", (r >= q) # Interprété comme r.__cmp__(q)
r.allonger(2) # r devient un rectangle 4×1
print "Aire de r après l'avoir allongé d'un facteur 2:", r.aire()
print "r >= q:", (r >= q)
Source : formes.py
VIII-C. Cercle circonscrit (POO, argparse)▲
Sélectionnez
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
159.
160.
161.
162.
163.
164.
165.
166.
167.
168.
169.
170.
171.
172.
173.
174.
175.
176.
177.
178.
179.
180.
181.
182.
183.
184.
185.
186.
187.
188.
189.
190.
191.
192.
193.
194.
195.
196.
197.
198.
199.
200.
201.
202.
203.
204.
205.
206.
207.
208.
209.
210.
211.
212.
213.
214.
215.
216.
217.
218.
219.
220.
221.
222.
223.
224.
225.
226.
227.
228.
229.
230.
231.
232.
233.
234.
235.
236.
237.
238.
239.
240.
241.
242.
243.
244.
245.
246.
247.
248.
249.
250.
251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
261.
262.
263.
264.
265.
266.
267.
268.
269.
270.
271.
272.
273.
274.
275.
276.
277.
278.
279.
280.
281.
282.
283.
284.
285.
286.
287.
288.
289.
290.
291.
292.
293.
294.
295.
296.
297.
298.
299.
300.
301.
302.
303.
304.
305.
306.
307.
308.
309.
310.
311.
312.
313.
314.
315.
316.
317.
318.
319.
320.
321.
322.
323.
324.
325.
326.
327.
328.
329.
330.
331.
332.
333.
334.
335.
336.
337.
338.
339.
340.
341.
342.
343.
344.
345.
346.
347.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
159.
160.
161.
162.
163.
164.
165.
166.
167.
168.
169.
170.
171.
172.
173.
174.
175.
176.
177.
178.
179.
180.
181.
182.
183.
184.
185.
186.
187.
188.
189.
190.
191.
192.
193.
194.
195.
196.
197.
198.
199.
200.
201.
202.
203.
204.
205.
206.
207.
208.
209.
210.
211.
212.
213.
214.
215.
216.
217.
218.
219.
220.
221.
222.
223.
224.
225.
226.
227.
228.
229.
230.
231.
232.
233.
234.
235.
236.
237.
238.
239.
240.
241.
242.
243.
244.
245.
246.
247.
248.
249.
250.
251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
261.
262.
263.
264.
265.
266.
267.
268.
269.
270.
271.
272.
273.
274.
275.
276.
277.
278.
279.
280.
281.
282.
283.
284.
285.
286.
287.
288.
289.
290.
291.
292.
293.
294.
295.
296.
297.
298.
299.
300.
301.
302.
303.
304.
305.
306.
307.
308.
309.
310.
311.
312.
313.
314.
315.
316.
317.
318.
319.
320.
321.
322.
323.
324.
325.
326.
327.
328.
329.
330.
331.
332.
333.
334.
335.
336.
337.
338.
339.
340.
341.
342.
343.
344.
345.
346.
347.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
Calcule le cercle circonscrit à 3 points du plan.
Ce script sert d'illustration à plusieurs concepts indépendants:
- un exemple de script (shebang, docstring, etc.) permettant une
utilisation en module (`import circonscrit`) et en exécutable
(`python circonscrit.py -h`);
- des exemples de Programmation Orientée Objet : classe `Point` et la
classe héritière `Vector`;
- un exemple d'utilisation du module `argparse` de la bibliothèque
standard, permettant la gestion des arguments de la ligne de
commande ;
- l'utilisation de tests unitaires sous la forme de `doctest` (tests
inclus dans les *docstrings* des éléments à tester).
Pour exécuter les tests unitaires du module :
- avec doctest: `python -m doctest -v circonscrit.py`
- avec pytests: `py.test --doctest-modules -v circonscrit.py`
- avec nose: `nosetests --with-doctest -v circonscrit.py`
"""
__author__ = "Yannick Copin <y.copin@ipnl.in2p3.fr>"
__version__ = "Time-stamp: <2014-01-12 22:19 ycopin@lyonovae03.in2p3.fr>"
# Définition d'une classe ==============================
class Point(object): # *object* est la classe dont dérivent toutes les autres
"""
Classe définissant un `Point` du plan, caractérisé par ses
coordonnées `x`,`y`.
"""
def __init__(self, x, y):
"""
Méthode d'instanciation à partir de deux coordonnées réelles.
>>> Point(0,1) # doctest: +ELLIPSIS
<circonscrit.Point object at 0x...>
>>> Point(1+3j)
Traceback (most recent call last):
...
TypeError: __init__() takes exactly 3 arguments (2 given)
"""
try: # Convertit les coords en `float`
self.x = float(x)
self.y = float(y)
except (ValueError, TypeError):
raise TypeError("Invalid input coordinates ({},{})".format(x, y))
def __str__(self):
"""
Surcharge de la fonction `str()`: l'affichage *informel* de l'objet
dans l'interpréteur, p.ex. `print self` sera résolu comme
`self.__str__()`
Retourne une chaîne de caractères.
>>> print Point(1,2)
Point (x=1.0, y=2.0)
"""
return "Point (x={p.x}, y={p.y})".format(p=self)
def isOrigin(self):
"""
Teste si le point est à l'origine en testant la nullité des deux
coordonnées.
Attention aux éventuelles erreurs d'arrondis: il faut tester
la nullité à la précision numérique près.
>>> Point(1,2).isOrigin()
False
>>> Point(0,0).isOrigin()
True
"""
import sys
eps = sys.float_info.epsilon # Le plus petit float non nul
return ((abs(self.x) <= eps) and (abs(self.y) <= eps))
def distance(self, other):
"""
Méthode de calcul de la distance du point (`self`) à un autre point
(`other`).
>>> A = Point(1,0); B = Point(1,1); A.distance(B)
1.0
"""
from math import hypot
return hypot(self.x - other.x, self.y - other.y) # sqrt(dx**2 + dy**2)
# Définition du point origine O
O = Point(0, 0)
# Héritage de classe ==============================
class Vector(Point):
"""
Un `Vector` hérite de `Point` avec des méthodes additionnelles
(p.ex. la négation d'un vecteur, l'addition de deux vecteurs, ou
la rotation d'un vecteur).
"""
def __init__(self, A, B):
"""
Définit le vecteur `AB` à partir des deux points `A` et `B`.
>>> Vector(Point(1,0), Point(1,1)) # doctest: +ELLIPSIS
<circonscrit.Vector object at 0x...>
>>> Vector(0, 1)
Traceback (most recent call last):
...
AttributeError: 'int' object has no attribute 'x'
"""
# Initialisation de la classe parente
Point.__init__(self, B.x - A.x, B.y - A.y)
# Attribut propre à la classe dérivée
self.sqnorm = self.x ** 2 + self.y ** 2 # Norme du vecteur au carré
def __str__(self):
"""
Surcharge de la fonction `str()`: `print self` sera résolu comme
`Vector.__str__(self)` (et non pas comme
`Point.__str__(self)`)
>>> A = Point(1,0); B = Point(1,1); print Vector(A,B)
Vector (x=0.0, y=1.0)
"""
return "Vector (x={v.x}, y={v.y})".format(v=self)
def __add__(self, other):
"""
Surcharge de l'opérateur binaire `{self} + {other}`: l'instruction
sera résolue comme `self.__add__(other)`.
On construit une nouvelle instance de `Vector` à partir des
coordonnées propres à l'objet `self` et à l'autre opérande
`other`.
>>> A = Point(1,0); B = Point(1,1)
>>> print Vector(A,B) + Vector(B,O) # = Vector(A,O)
Vector (x=-1.0, y=0.0)
"""
return Vector(O, Point(self.x + other.x, self.y + other.y))
def __sub__(self, other):
"""
Surcharge de l'opérateur binaire `{self} - {other}`: l'instruction
sera résolue comme `self.__sub__(other)`.
Attention: ne surcharge pas l'opérateur unaire `-{self}`, géré
par `__neg__`.
>>> A = Point(1,0); B = Point(1,1)
>>> print Vector(A,B) - Vector(A,B) # Différence
Vector (x=0.0, y=0.0)
>>> -Vector(A,B) # Négation
Traceback (most recent call last):
...
TypeError: bad operand type for unary -: 'Vector'
"""
return Vector(O, Point(self.x - other.x, self.y - other.y))
def __eq__(self, other):
"""
Surcharge du test d'égalité `{self}=={other}`: l'instruction sera
résolue comme `self.__eq__(other)`.
>>> Vector(O,Point(0,1)) == Vector(Point(1,0),Point(1,1))
True
"""
# On teste ici la nullité de la différence des 2
# vecteurs. D'autres tests auraient été possibles -- égalité
# des coordonnées, nullité de la norme de la différence,
# etc. -- mais on tire profit de la méthode héritée
# `Point.isOrigin()` testant la nullité des coordonnées (à la
# précision numérique près).
return (self - other).isOrigin()
def __abs__(self):
"""
Surcharge la fonction `abs()` pour retourner la norme du vecteur.
>>> abs(Vector(Point(1,0), Point(1,1)))
1.0
"""
# On pourrait utiliser sqrt(self.sqnorm), mais c'est pour
# illustrer l'utilisation de la méthode héritée
# `Point.distance`...
return Point.distance(self, O)
def rotate(self, angle, deg=False):
"""
Rotation (dans le sens trigonométrique) du vecteur par un `angle`,
exprimé en radians ou en degrés.
>>> Vector(Point(1,0),Point(1,1)).rotate(90,deg=True) == Vector(O,Point(-1,0))
True
"""
from cmath import rect # Bibliothèque de fonctions complexes
# On calcule la rotation en passant dans le plan complexe
z = complex(self.x, self.y)
phase = angle if not deg else angle / 57.29577951308232 # [rad]
u = rect(1., phase) # exp(i*phase)
zu = z * u # Rotation complexe
return Vector(O, Point(zu.real, zu.imag))
def circumscribedCircle(M, N, P):
"""
Calcule le centre et le rayon du cercle circonscrit aux points
M,N,P.
Retourne: (centre [Point],rayon [float])
Lève une exception `ValueError` si le rayon ou le centre du cercle
circonscrit n'est pas défini.
>>> M = Point(-1,0); N = Point(1,0); P = Point(0,1)
>>> C,r = circumscribedCircle(M,N,P) # Centre O, rayon 1
>>> print C.distance(O), r
0.0 1.0
>>> circumscribedCircle(M,O,N) # Indéfini
Traceback (most recent call last):
...
ValueError: Undefined circumscribed circle radius.
"""
from math import sqrt
MN = Vector(M, N)
NP = Vector(N, P)
PM = Vector(P, M)
# Rayon du cercle circonscrit
m = abs(NP) # |NP|
n = abs(PM) # |PM|
p = abs(MN) # |MN|
d = (m + n + p) * (-m + n + p) * (m - n + p) * (m + n - p)
if d > 0:
rad = m * n * p / sqrt(d)
else:
raise ValueError("Undefined circumscribed circle radius.")
# Centre du cercle circonscrit
d = -2 * (M.x * NP.y + N.x * PM.y + P.x * MN.y)
if d == 0:
raise ValueError("Undefined circumscribed circle center.")
om2 = Vector(O, M).sqnorm # |OM|**2
on2 = Vector(O, N).sqnorm # |ON|**2
op2 = Vector(O, P).sqnorm # |OP|**2
x0 = -(om2 * NP.y + on2 * PM.y + op2 * MN.y) / d
y0 = (om2 * NP.x + on2 * PM.x + op2 * MN.x) / d
return (Point(x0, y0), rad) # (centre [Point], R [float])
if __name__ == '__main__':
# start-argparse
import argparse
parser = argparse.ArgumentParser(
usage="%(prog)s [-p/--plot] [-i/--input coordfile | x1,y1 x2,y2 x3,y3]",
description=__doc__)
parser.add_argument('coords', nargs='*', type=str, metavar='x,y',
help="Coordinates of point")
parser.add_argument('-i', '--input', nargs='?', type=file,
help="Coordinate file (one 'x,y' per line)")
parser.add_argument('-p', '--plot', action="store_true", default=False,
help="Draw the circumscribed circle")
parser.add_argument('--version', action='version', version=__version__)
args = parser.parse_args()
# end-argparse
if args.input: # Lecture des coordonnées du fichier d'entrée
# Le fichier a déjà été ouvert en lecture par argparse (type=file)
args.coords = [coords for coords in args.input
if not coords.strip().startswith('#')]
if len(args.coords) != 3: # Vérifie le nb de points
parser.error("Specify 3 points by their coordinates 'x,y' (got {})"
.format(len(args.coords)))
points = [] # Liste des points
for i, arg in enumerate(args.coords, start=1):
try: # Déchiffrage de l'argument 'x,y'
x, y = (float(t) for t in arg.split(','))
except ValueError:
parser.error(
"Cannot decipher coordinates #{}: '{}'".format(i, arg))
points.append(Point(x, y)) # Création du point et ajout à la liste
print "#{:d}: {}".format(i, points[-1]) # Affichage du dernier point
# Calcul du cercle cisconscrit (lève une ValueError en cas de problème)
center, radius = circumscribedCircle(*points) # Délistage
print "Circumscribed circle: {}, radius: {}".format(center, radius)
if args.plot: # Figure
import matplotlib.pyplot as P
fig = P.figure()
ax = fig.add_subplot(1, 1, 1, aspect='equal')
# Points
ax.plot([p.x for p in points], [p.y for p in points], 'ko')
for i, p in enumerate(points, start=1):
ax.annotate("#{}".format(i), (p.x, p.y),
xytext=(5, 5), textcoords='offset points')
# Cercle circonscrit
c = P.matplotlib.patches.Circle((center.x, center.y), radius=radius,
fc='none', ec='k')
ax.add_patch(c)
ax.plot(center.x, center.y, 'r+')
P.show()
Sélectionnez
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
$ ./circonscrit.py -h
usage: circonscrit.py [-p/--plot] [-i/--input coordfile | x1,y1 x2,y2 x3,y3]
positional arguments:
x,y Coordinates of point
optional arguments:
-h, --help show this help message and exit
-i [INPUT], --input [INPUT]
Coordinate file (one 'x,y' per line)
-p, --plot Draw the circumscribed circle
--version show program's version number and exit
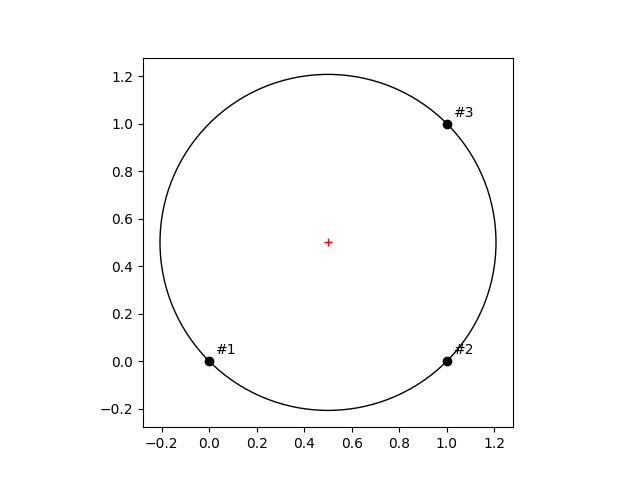
$ ./circonscrit.py -p 0,0 1,0 1,1
Source : circonscrit.py
VIII-D. Matplotlib▲
VIII-D-1. Figure (relativement) simple▲
Sélectionnez
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Time-stamp: <2014-12-15 16:06:44 ycopin>
"""
Exemple un peu plus complexe de figure, incluant 2 axes, légendes, axes, etc.
"""
import numpy as N
import matplotlib.pyplot as P
try:
import seaborn # Amélioration de la charte graphique
except ImportError:
print u"Seaborn n'est pas accessible, charte graphique par défaut."
x = N.linspace(-N.pi, 3*N.pi, 2*360)
# Signal carré
y = N.sign(N.sin(x)) # = ± 1
# 3 premiers termes de la décomposition en série de Fourier
y1 = 4/N.pi * N.sin(x) # Fondamentale
y2 = 4/N.pi * N.sin(3*x) / 3 # 1re harmonique
y3 = 4/N.pi * N.sin(5*x) / 5 # 2de harmonique
# Somme des 3 premières composantes
ytot = y1 + y2 + y3
# Figure
fig = P.figure() # Création de la Figure
# 1er axe: composantes
ax1 = fig.add_subplot(2, 1, 1, # 1er axe d'une série de 2 × 1
ylabel="Composantes",
title=u"Décomposition en série de Fourier")
ax1.plot(x, y1, label="Fondamental")
ax1.plot(x, y2, label=u"1re harmonique")
ax1.plot(x, y3, label=u"2de harmonique")
ax1.legend(loc="upper left", fontsize="x-small")
# 2nd axe: décomposition
ax2 = fig.add_subplot(2, 1, 2, # 2d axe d'une série de 2 × 1
ylabel=u"Décomposition",
xlabel="x [rad]")
ax2.plot(x, y, lw=2, color='k', label=u"Signal carré")
ax2.plot(x, ytot, lw=2, ls=':', color='k', label=u"Somme des composantes")
ax2.legend(loc="upper left", fontsize="x-small")
# Sauvegarde de la figure (pas d'affichage intéractif)
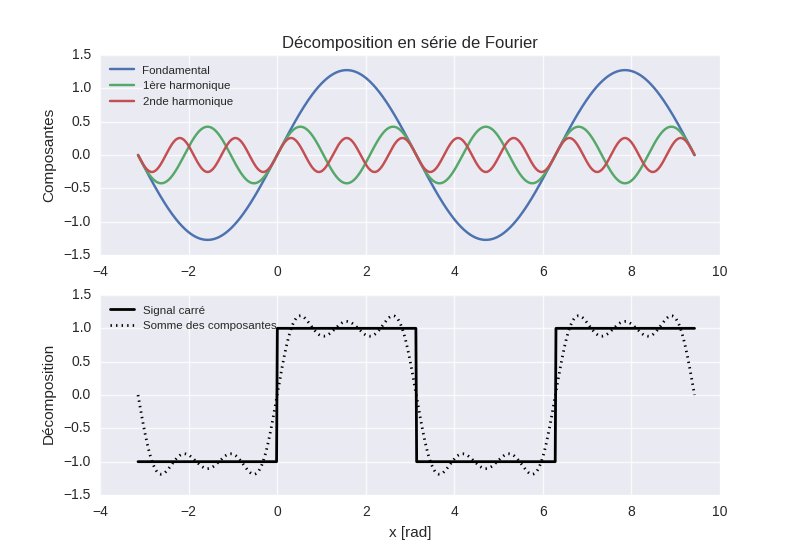
fig.savefig("figure.png")
Source : figure.py
VIII-D-2. Filtres du 2d ordre▲
Sélectionnez
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as N
import matplotlib.pyplot as P
def passeBas(x, Q=1):
"""
Filtre passe-bas en pulsation réduite *x* = omega/omega0, facteur de
qualité *Q*.
"""
return 1 / (1 - x ** 2 + x / Q * 1j)
def passeHaut(x, Q=1):
return -x ** 2 / (1 - x ** 2 + x / Q * 1j)
def passeBande(x, Q=1):
return 1 / (1 + Q * (x - 1 / x) * 1j)
def coupeBande(x, Q=1):
return (1 - x ** 2) / (1 - x ** 2 + x / Q * 1j)
def gainNphase(f, dB=True):
"""
Retourne le gain (éventuellement en dB) et la phase [rad] d'un
filtre de fonction de transfert complexe *f*.
"""
g = N.abs(f) # Gain
if dB: # [dB]
g = 20 * N.log10(g)
p = N.angle(f) # [rad]
return g, p
def asympGain(x, pentes=(0, -40)):
lx = N.log10(x)
return N.where(lx < 0, pentes[0] * lx, pentes[1] * lx)
def asympPhase(x, phases=(0, -N.pi)):
return N.where(x < 1, phases[0], phases[1])
def diagBode(x, filtres, labels,
title='', plim=None, gAsymp=None, pAsymp=None):
"""
Trace le diagramme de Bode -- gain [dB] et phase [rad] -- des filtres
de fonction de transfert complexe *filtres* en fonction de la pulsation
réduite *x*.
"""
fig = P.figure()
axg = fig.add_subplot(2, 1, 1, # Axe des gains
xscale='log',
ylabel='Gain [dB]')
axp = fig.add_subplot(2, 1, 2, # Axe des phases
sharex=axg,
xlabel=r'x = $\omega$/$\omega_0$', xscale='log',
ylabel='Phase [rad]')
lstyles = ['--', '-', '-.', ':']
for f, label, ls in zip(filtres, labels, lstyles): # Tracé des courbes
g, p = gainNphase(f, dB=True) # Calcul du gain et de la phase
axg.plot(x, g, lw=2, ls=ls, label="Q=" + str(label)) # Gain
axp.plot(x, p, lw=2, ls=ls) # Phase
# Asymptotes
if gAsymp is not None: # Gain
axg.plot(x, asympGain(x, gAsymp), 'k:', lw=2, label='_')
if pAsymp is not None: # Phase
#axp.plot(x, asympPhase(x,pAsymp), 'k:')
pass
axg.legend(loc='best', prop=dict(size='small'))
# Labels des phases
axp.set_yticks(N.arange(-2, 2.1) * N.pi / 2)
axp.set_yticks(N.arange(-4, 4.1) * N.pi / 4, minor=True)
axp.set_yticklabels([r'$-\pi$', r'$-\pi/2$', r'$0$', r'$\pi/2$', r'$\pi$'])
# Domaine des phases
if plim is not None:
axp.set_ylim(plim)
# Ajouter les grilles
for ax in (axg, axp):
ax.grid() # x et y, majors
ax.grid(which='minor') # x et y, minors
# Ajustements fins
gmin, gmax = axg.get_ylim()
axg.set_ylim(gmin, max(gmax, 3))
fig.subplots_adjust(hspace=0.1)
axg.xaxis.set_major_formatter(P.matplotlib.ticker.ScalarFormatter())
P.setp(axg.get_xticklabels(), visible=False)
if title:
axg.set_title(title)
return fig
if __name__ == '__main__':
#P.rc('mathtext', fontset='stixsans')
x = N.logspace(-1, 1, 1000) # de 0.1 à 10 en 1000 pas
# Facteurs de qualité
qs = [0.25, 1 / N.sqrt(2), 5] # Valeurs numériques
labels = [0.25, r'$1/\sqrt{2}$', 5] # Labels
# Calcul des fonctions de transfert complexes
pbs = [ passeBas(x, Q=q) for q in qs ]
phs = [ passeHaut(x, Q=q) for q in qs ]
pcs = [ passeBande(x, Q=q) for q in qs ]
cbs = [ coupeBande(x, Q=q) for q in qs ]
# Création des 4 diagrammes de Bode
figPB = diagBode(x, pbs, labels, title='Filtre passe-bas',
plim=(-N.pi, 0),
gAsymp=(0, -40), pAsymp=(0, -N.pi))
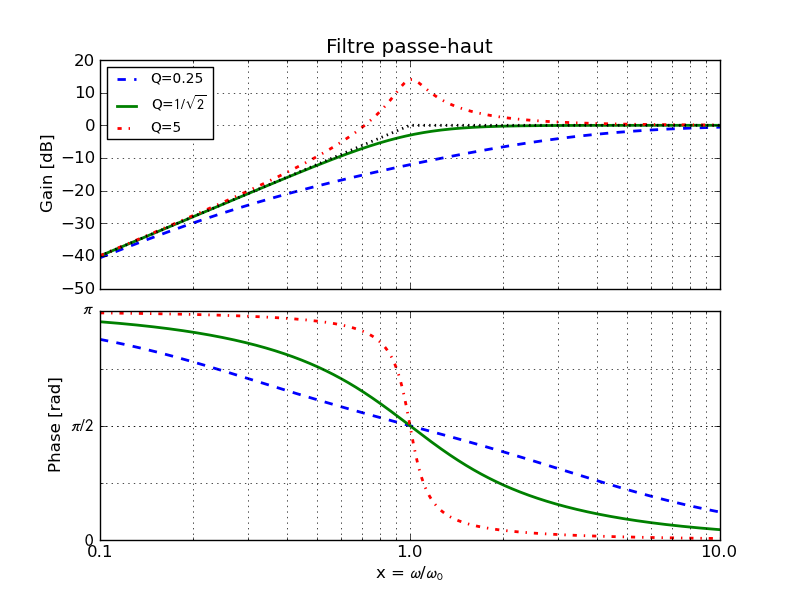
figPH = diagBode(x, phs, labels, title='Filtre passe-haut',
plim=(0, N.pi),
gAsymp=(40, 0), pAsymp=(N.pi, 0))
figPC = diagBode(x, pcs, labels, title='Filtre passe-bande',
plim=(-N.pi / 2, N.pi / 2),
gAsymp=(20, -20), pAsymp=(N.pi / 2, -N.pi / 2))
figCB = diagBode(x, cbs, labels, title='Filtre coupe-bande',
plim=(-N.pi / 2, N.pi / 2),
gAsymp=(0, 0), pAsymp=(0, 0))
P.show()
Source : filtres2ndOrdre.py